


Next: HADRON STRUCTUUR
Up: HADRON STRUCTUUR
Previous: Werkzame Doorsnede
Werkzame Doorsneden en Matrixelementen
Uit de quantummechanica volgt25
dat de werkzame doorsnede voor de reactie
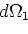 |
(36) |
berekend kan worden uit het matrixelement 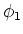 voor de overgang
van de begintoestand
voor de overgang
van de begintoestand 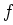 naar de eindtoestand
naar de eindtoestand 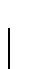 . Er geldt26
. Er geldt26
In bovenstaande vergelijking hebben we weer alle spinfactoren
weggelaten. De relatieve snelheid van de deeltjes in de
begintoestand wordt aangegeven met  .
We dienen te integreren over alle niet gemeten variabelen.
.
We dienen te integreren over alle niet gemeten variabelen.
Figure 31:
Schematische voorstelling van de botsing van een bundel- en een
targetdeeltje in het zwaartepuntsysteem.
|
Ter vereenvoudiging rekenen we met slechts twee deeltjes in de
eindtoestand en gebruiken we de niet-relativistische kinematica in
het zwaartepuntsysteem (zie figuur 31). Integratie over
 geeft
geeft
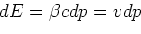 |
(38) |
Na een verdere integratie27 over  krijgen we
krijgen we
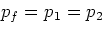 |
(39) |
waarbij 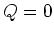 de impuls van de eindtoestand is28.
de impuls van de eindtoestand is28.
Indien we verder even aannemen dat 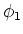 constant is29, dan kunnen we enkele uitspraken doen over het gedrag
van de werkzame doorsnede in de buurt van een drempel.
We kunnen drie gevallen onderscheiden.
constant is29, dan kunnen we enkele uitspraken doen over het gedrag
van de werkzame doorsnede in de buurt van een drempel.
We kunnen drie gevallen onderscheiden.
-
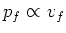 , elastische verstrooiing. Omdat
, elastische verstrooiing. Omdat
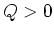 is de werkzame doorsnede constant (onafhankelijk van de
energie en de verstrooiingshoek).
is de werkzame doorsnede constant (onafhankelijk van de
energie en de verstrooiingshoek).
-
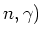 , bijvoorbeeld (
, bijvoorbeeld (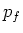 reacties. Voor lage
energieën zijn de veranderingen in
reacties. Voor lage
energieën zijn de veranderingen in 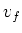 en
en 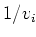 uiterst klein.
De werkzame doorsnede is daarom evenredig met
uiterst klein.
De werkzame doorsnede is daarom evenredig met 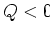 .
.
-
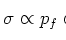 , bijvoorbeeld in reacties waarbij deeltjes
geproduceerd worden. In dit
geval is de reactie voor lage energieën verboden. Boven de drempel
neemt de werkzame doorsnede snel toe,
, bijvoorbeeld in reacties waarbij deeltjes
geproduceerd worden. In dit
geval is de reactie voor lage energieën verboden. Boven de drempel
neemt de werkzame doorsnede snel toe,
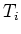 (
(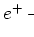 is de kinetische energie in de
begintoestand).
is de kinetische energie in de
begintoestand).
Figure 32:
Verhouding van de werkzame doorsneden voor de productie van
twee deeltjes met tegenovergestelde lading in de reactie
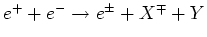 en de werkzame doorsnede
voor de productie van
en de werkzame doorsnede
voor de productie van 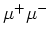 paren. Hierbij is
paren. Hierbij is 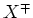 een
geladen lepton of meson en
een
geladen lepton of meson en 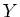 symboliseert niet-gedetecteerde
neutrale deeltjes. De scherpe toename bij 3.55 GeV
is afkomstig van
symboliseert niet-gedetecteerde
neutrale deeltjes. De scherpe toename bij 3.55 GeV
is afkomstig van 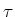 -paarproductie.
-paarproductie.
|
Figuur 32 toont een voorbeeld van het
gedrag van de werkzame doorsnede
als functie van de bundelenergie in de buurt van een drempel.
Dit wordt gedemonsteerd aan de hand van het proces
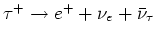 . De
. De 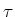 leptonen vervallen
via de reacties
leptonen vervallen
via de reacties
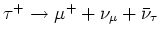 of
of
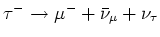 , en
, en
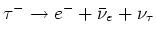 , of
, of
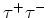 . De neutrino's die
in het proces worden gecreëerd worden niet gedetecteerd. De drempel
voor
. De neutrino's die
in het proces worden gecreëerd worden niet gedetecteerd. De drempel
voor 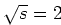 productie, en dus de massa van het
productie, en dus de massa van het 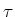 lepton,
volgt uit de toename van de werkzame doorsnede met toenemende
energie in het zwaartepuntsysteem. Het experimentele resultaat voor
de drempelwaarde bij
lepton,
volgt uit de toename van de werkzame doorsnede met toenemende
energie in het zwaartepuntsysteem. Het experimentele resultaat voor
de drempelwaarde bij
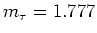 impliceert een
massa van
impliceert een
massa van
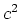 GeV/
GeV/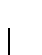 .
.
Als eerste voorbeeld van het gebruik van relatie (112)
schatten we de werkzame doorsnede voor de reactie
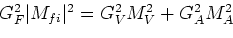 |
(40) |
Hierbij gebruiken we de koppelingsconstante van de zwakke
wisselwerking die we reeds vroeger uit deeltjesverval bepaald
hebben30.
Voor een inkomende antineutrino-energie van
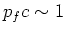 MeV vinden we
MeV vinden we 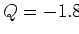 MeV (de
MeV (de 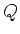 -waarde
van de reactie bedraagt MeV). De werkzame doorsnede bedraagt
-waarde
van de reactie bedraagt MeV). De werkzame doorsnede bedraagt



Next: HADRON STRUCTUUR
Up: HADRON STRUCTUUR
Previous: Werkzame Doorsnede
Jo van den Brand
2002-03-25
![]() geeft
geeft
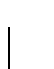 krijgen we
krijgen we
![]() constant is29, dan kunnen we enkele uitspraken doen over het gedrag
van de werkzame doorsnede in de buurt van een drempel.
We kunnen drie gevallen onderscheiden.
constant is29, dan kunnen we enkele uitspraken doen over het gedrag
van de werkzame doorsnede in de buurt van een drempel.
We kunnen drie gevallen onderscheiden.
![]() . De
. De ![]() leptonen vervallen
via de reacties
leptonen vervallen
via de reacties
![]() of
of
![]() , en
, en
![]() , of
, of
![]() . De neutrino's die
in het proces worden gecreëerd worden niet gedetecteerd. De drempel
voor
. De neutrino's die
in het proces worden gecreëerd worden niet gedetecteerd. De drempel
voor ![]() productie, en dus de massa van het
productie, en dus de massa van het ![]() lepton,
volgt uit de toename van de werkzame doorsnede met toenemende
energie in het zwaartepuntsysteem. Het experimentele resultaat voor
de drempelwaarde bij
lepton,
volgt uit de toename van de werkzame doorsnede met toenemende
energie in het zwaartepuntsysteem. Het experimentele resultaat voor
de drempelwaarde bij
![]() impliceert een
massa van
impliceert een
massa van
![]() GeV/
GeV/![]() .
.