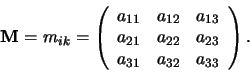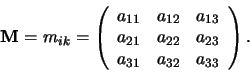Matrices en operatoren

Een kwadratische matrix kan voorgesteld worden door een kwadratisch getallenschema. Bijvoorbeeld voor $n=3$,

$${\bf M} = m_{ik} = \left( \begin{array}{ccc} a_{11} & a_{... ...{23} \\ a_{31} & a_{32} & a_{33} \\ \end{array} \right).$$ (320)

De belangrijkste matrixoperatie is de vermenigvuldiging met een vector ${\bf a}$. Het resultaat van deze operatie is een andere vector: ${\bf b} = {\bf Ma} = m_{ik}a_k$, waarbij deze vector ${\bf b}$ als componenten $b_{i} = \sum_{k=1}^n m_{ik}a_k$ heeft. De component $i$ is het inproduct van rij $i$ van de matrix met de vector ${\bf a}$. Men kan ook stellen dat de matrix ${\bf M}$ uit de vector ${\bf a}$ een andere vector ${\bf b}$ genereert. Preciezer geformuleerd is de matrix een lineaire vectorfunctie. Hiermee wordt bedoeld dat net zoals een functie ${\bf f}$ aan elk getal $x$ een ander getal $f(x)$ toevoegt, voegt een matrix aan elke vector ${\bf a}$ een andere vector ${\bf b} = {\bf Ma}$ toe. Lineair betekent in dit verband dat in het algemeen geldt dat

$${\bf M} ({\bf a}+{\bf b}) = {\bf Ma} + {\bf Mb}.$$ (321)

Een operator is voor functies hetzelfde als een matrix is voor vectoren. Een operator ${\bf A}$ genereert uit elke functie ${\bf f}$ een andere functie ${\bf g} = {\bf Af}$. Preciezer geformuleerd voegt een lineaire operator aan elke functie ${\bf f}$ een andere functie ${\bf g} = {\bf Af}$ toe, waarbij

$${\bf A} ({\bf f}_1+{\bf f}_2) = {\bf Af}_1 + {\bf Af}_2.$$ (322)

Andere voorbeelden van operatoren worden gegeven in tabel 3.

Tabel 3: Enkele voorbeelden van operatoren die werken op een functie en hieruit een nieuwe functie genereren.

Voorbeeld	Actie
Additie van een constante	${\bf Af} = {\bf f}+a$
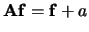Vermenigvuldiging met een constante	${\bf Af} = a{\bf f}$
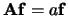Vermenigvuldiging met $x$	${\bf Af} = x{\bf f}$
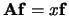Differentiëren naar $x$	${\bf Af} = {d \over dx} {\bf f}$
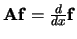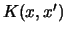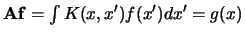Integraaloperator met `kernel' $K(x,x^\prime )$	${\bf Af} = \int K(x,x^\prime )f(x^\prime ) dx^\prime =g(x)$