



Next: Grondslagen van de quantummechanica
Up: Operatoren en complexe functies
Previous: Matrices en operatoren
Contents
Een operator heeft op een functie, net zoals een matrix dat heeft op
een vector, in het algemeen twee acties: hij strekt de functie (verandert
de lengte) en hij roteert de functie (verandert de richting). Voor deze
rotatie zijn er bij oneindig veel dimensies buitengewoon veel mogelijkheden.
Van belang zijn vooral die gevallen waarbij een rotatie achterwege blijft,
waarbij de functie 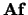 parallel is aan de functie
parallel is aan de functie 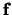 ,
,
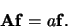 |
(323) |
Functies die door een gegeven operator niet geroteerd worden heten
de eigenfuncties van die operator. De bijbehorende waarden van
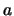 heten de eigenwaarden van de operator. Als er bij dezelfde
eigenwaarde meerdere eigenfuncties horen, dan noemt men die eigenwaarden
en eigenfuncties ontaard.
heten de eigenwaarden van de operator. Als er bij dezelfde
eigenwaarde meerdere eigenfuncties horen, dan noemt men die eigenwaarden
en eigenfuncties ontaard.
In de quantummechanica is een speciale klasse van operatoren van
bijzonder belang: de Hermitische operatoren. Een Hermitisch
operator voldoet aan de definitie
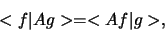 |
(324) |
voor alle functie 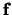 en
en 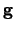 .
De eigenfuncties en eigenwaarden van Hermitische operatoren hebben een
aantal belangrijke eigenschappen. De eigenwaarden van een Hermitische
operator zijn reëel en de eigenvectoren die horen bij
verschillende eigenwaarden zijn orthogonaal. De derde eigenschap,
compleetheid van de eigenvectoren, is in het algemeen slechts
geldig in een eindig-dimensionale ruimte. In oneindig dimensionale
ruimten hebben sommige Hermitische operatoren een complete verzameling
eigenvectoren, sommige hebben een niet-complete verzameling, en
sommige hebben helemaal geen eigenvectoren in die ruimte. In de
quantum fysica is de eigenschap van compleetheid absoluut essentieel en
de eigenfuncties van de meest voorkomende Hermitische operatoren hebben
behalve hun orthogonaliteit deze belangrijke eigenschap van
volledigheid: men kan elke willekeurige functie ontwikkelen
in deze eigenfuncties, net zoals men functies kan Fourier-ontwikkelen naar
de eveneens orthogonale functies
.
De eigenfuncties en eigenwaarden van Hermitische operatoren hebben een
aantal belangrijke eigenschappen. De eigenwaarden van een Hermitische
operator zijn reëel en de eigenvectoren die horen bij
verschillende eigenwaarden zijn orthogonaal. De derde eigenschap,
compleetheid van de eigenvectoren, is in het algemeen slechts
geldig in een eindig-dimensionale ruimte. In oneindig dimensionale
ruimten hebben sommige Hermitische operatoren een complete verzameling
eigenvectoren, sommige hebben een niet-complete verzameling, en
sommige hebben helemaal geen eigenvectoren in die ruimte. In de
quantum fysica is de eigenschap van compleetheid absoluut essentieel en
de eigenfuncties van de meest voorkomende Hermitische operatoren hebben
behalve hun orthogonaliteit deze belangrijke eigenschap van
volledigheid: men kan elke willekeurige functie ontwikkelen
in deze eigenfuncties, net zoals men functies kan Fourier-ontwikkelen naar
de eveneens orthogonale functies 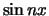 en
en  .
Op deze generalisatie van de Fourier-ontwikkeling berusten de meeste
benaderingsmethoden die gebruikt worden in de quantummechanica.
We zullen later zien hoe we hier mee omgaan.
.
Op deze generalisatie van de Fourier-ontwikkeling berusten de meeste
benaderingsmethoden die gebruikt worden in de quantummechanica.
We zullen later zien hoe we hier mee omgaan.




Next: Grondslagen van de quantummechanica
Up: Operatoren en complexe functies
Previous: Matrices en operatoren
Contents
Jo van den Brand
2004-09-25