



Next: Matrices en operatoren
Up: Operatoren en complexe functies
Previous: Inleiding
Contents
We beschouwen de verzameling 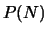 van alle polynomen
van de graad
van alle polynomen
van de graad 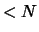 ,
,
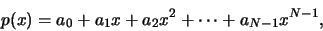 |
(314) |
op het interval
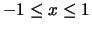 . De functies zijn op dit domein
zeker kwadratisch integreerbaar en we hebben dus een bona fide
inproduct ruimte. Een voor de hand liggende basis is de verzameling
. De functies zijn op dit domein
zeker kwadratisch integreerbaar en we hebben dus een bona fide
inproduct ruimte. Een voor de hand liggende basis is de verzameling
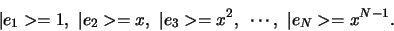 |
(315) |
We hebben duidelijk te maken met een 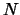 -dimensionale vector ruimte.
De basis is echter niet orthonormaal, want we zien bijvoorbeeld direct dat
-dimensionale vector ruimte.
De basis is echter niet orthonormaal, want we zien bijvoorbeeld direct dat
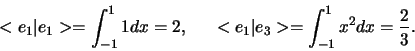 |
(316) |
We kunnen nu de Gram-Schmidt procedure toepassen, teneinde de basis
te orthonormaliseren. Als we dat doen vinden we de Legendre
polynomen, 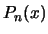 , behalve dan dat Legendre niet zo op de
normering gelet heeft,
, behalve dan dat Legendre niet zo op de
normering gelet heeft,
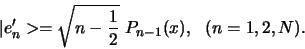 |
(317) |
De eerste paar Legendre polynomen worden in table 2
getoond.
Tabel 2:
Enkele van de eerste Legendre polynomen, 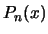 .
.
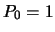 |
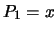 |
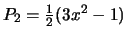 |
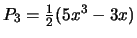 |
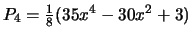 |
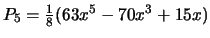 |
Als tweede voorbeeld beschouwen we de
verzameling 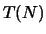 van alle goniometrische functies van de vorm
van alle goniometrische functies van de vorm
![\begin{displaymath}
f(x) = \sum_{n=0}^{N-1} \left[ a_n \sin{(n\pi x)} + b_n\cos{(n\pi x)} \right] ,
\end{displaymath}](img1066.png) |
(318) |
op het interval
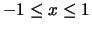 . Ook nu kunnen we laten zien dat
. Ook nu kunnen we laten zien dat
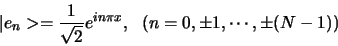 |
(319) |
een orthonormale basis vertegenwoordigt. Hierdoor kunnen we een willekeurige
functie schrijven als een lineaire combinatie van deze basis functies. Hierop
berust de Fourieranalyse.




Next: Matrices en operatoren
Up: Operatoren en complexe functies
Previous: Inleiding
Contents
Jo van den Brand
2004-09-25
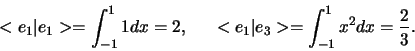
![]() van alle goniometrische functies van de vorm
van alle goniometrische functies van de vorm
![\begin{displaymath}
f(x) = \sum_{n=0}^{N-1} \left[ a_n \sin{(n\pi x)} + b_n\cos{(n\pi x)} \right] ,
\end{displaymath}](img1066.png)