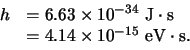Next: Fotoelektrisch effect
Up: DEELTJES EN GOLVEN
Previous: Dynamica van deeltjes
Contents
In 1905 poneerde Einstein de hypothese dat licht zich
onder bepaalde omstandigheden kan gedragen alsof haar energie
geconcentreerd is in discrete hoeveelheden die hij licht quanta
noemde; we noemen dat fotonen. Hij stelde voor dat de
energie van een enkel foton gegeven is door
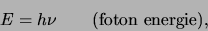 |
(77) |
waarbij 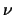 de frequentie van het licht is en
de frequentie van het licht is en 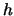 de
constante van Planck. Deze constante werd door Planck aan het
begin van deze eeuw geïntroduceerd in de fysica en heeft de waarde
de
constante van Planck. Deze constante werd door Planck aan het
begin van deze eeuw geïntroduceerd in de fysica en heeft de waarde
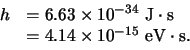 |
(78) |
Fotonen dragen niet alleen energie, maar ook impuls. Deze kan
gevonden worden door gebruik te maken van de relativistische relatie
tussen energie en impuls,
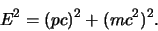 |
(79) |
We passen bovenstaande uitdrukking toe op een foton door te stellen
dat 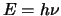 en
en 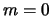 , omdat een foton dat met de lichtsnelheid
reist geen rustmassa kan hebben. We vinden dan
, omdat een foton dat met de lichtsnelheid
reist geen rustmassa kan hebben. We vinden dan 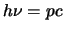 en met
en met
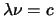 geeft dat
geeft dat
 |
(80) |
waarbij 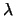 de golflengte van het licht is.
Merk op dat het golf- en deeltjesmodel met elkaar in verband staan.
De energie
de golflengte van het licht is.
Merk op dat het golf- en deeltjesmodel met elkaar in verband staan.
De energie 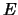 is gerelateerd aan de frequentie
is gerelateerd aan de frequentie 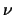 , en de
impuls
, en de
impuls 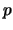 aan de golflengte
aan de golflengte 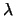 . In beide gevallen wordt
de evenredigheidsconstante gegeven door de constante van Planck,
. In beide gevallen wordt
de evenredigheidsconstante gegeven door de constante van Planck, 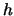 .
.
Tabel 1:
Elektromagnetisch spectrum en bijbehorende golflengten,
frequenties en foton energieën.
| Gebied |
Golflengte |
Frequentie |
Foton energie |
| |
|
[ Hz ] |
|
| Gammastraling |
50 fm |
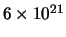 |
25 MeV |
| X-ray (Rontgenstraling) |
50 pm |
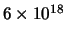 |
25 keV |
| Ultraviolet |
100 nm |
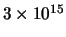 |
12 eV |
| Zichtbaar |
550 nm |
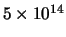 |
2 eV |
| Infrarood |
10 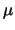 m m |
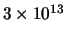 |
120 meV |
| Microgolven |
1 cm |
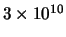 |
120 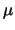 eV eV |
| Radiogolven |
1 km |
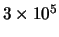 |
1.2 neV |
Gewapend met deze kennis kijken we nu eens naar het elektromagnetische
spectrum (zie tabel 1). We zien dat het zichtbare licht
slechts een klein deel van het spectrum bestrijkt. De gevoeligheid
van het oog is maximaal voor 550 nm en neemt af tot 1 % van de
maximale waarde bij 430 en 690 nm. Als het donker is, dan verandert
de gevoeligheid; het maximum ligt dan bij ongeveer 500 nm.
Aan het begin van de eeuw waren fysici zeer tevreden met de golftheorie
van licht en hadden moeite om Einstein's fotonen te accepteren.
In zijn aanbeveling voor de toelating van Einstein tot de
Koninklijke Pruisische Academie voor Wetenschappen schreef Planck
in 1913: `..dat hij soms de plank heeft misgeslagen met zijn
speculaties, zoals bijvoorbeeld in zijn theorie van lichtquanta,
dient niet echt tegen hem gebruikt te worden.'




Next: Fotoelektrisch effect
Up: DEELTJES EN GOLVEN
Previous: Dynamica van deeltjes
Contents
Jo van den Brand
2004-09-25