



Next: Quantummechanica en leven
Up: Klassieke fysica en werkelijkheid
Previous: Klassieke fysica en werkelijkheid
Contents
Quantummechanica heeft een nieuw concept ingevoerd met betrekking
tot de toestand van een systeem. Er wordt nog steeds gesproken
over deeltjes, maar niet meer over exacte posities en snelheden
er van. Er wordt met toestandfuncties, 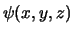 , gewerkt,
die bepaalde waarden hebben voor alle posities van een
systeem. Deze toestanden geven een beschrijving van de realiteit,
maar ze laten geen voorspelling toe van posities en snelheden
in het verleden of in de toekomst. Er bestaan echter eenvoudige
mathematische procedures die een berekening toestaan van
verwachtingswaarden van alle metingen die men op een dergelijk systeem
zou kunnen uitvoeren. Soms wordt gesteld dat quantummechanica
een berekening van de waarschijnlijkheid mogelijk maakt, dat een
bepaalde grootheid van een systeem, zoals impuls, in een meting een
bepaalde waarde heeft. Dat is echter een ongelukkige uitdrukking,
want quantummechanica spreekt niet over grootheden van een systeem.
Quantummechanica doet zelfs geen uitspraak over eventuele grootheden
die een systeem zou bezitten, maar zegt in termen van waarschijnlijkheid,
wat men zou kunnen vinden
indien een bepaalde meting wordt uitgevoerd. Kennis van de golffunctie
vertegenwoordigt de maximale kennis die men van een systeem kan hebben.
, gewerkt,
die bepaalde waarden hebben voor alle posities van een
systeem. Deze toestanden geven een beschrijving van de realiteit,
maar ze laten geen voorspelling toe van posities en snelheden
in het verleden of in de toekomst. Er bestaan echter eenvoudige
mathematische procedures die een berekening toestaan van
verwachtingswaarden van alle metingen die men op een dergelijk systeem
zou kunnen uitvoeren. Soms wordt gesteld dat quantummechanica
een berekening van de waarschijnlijkheid mogelijk maakt, dat een
bepaalde grootheid van een systeem, zoals impuls, in een meting een
bepaalde waarde heeft. Dat is echter een ongelukkige uitdrukking,
want quantummechanica spreekt niet over grootheden van een systeem.
Quantummechanica doet zelfs geen uitspraak over eventuele grootheden
die een systeem zou bezitten, maar zegt in termen van waarschijnlijkheid,
wat men zou kunnen vinden
indien een bepaalde meting wordt uitgevoerd. Kennis van de golffunctie
vertegenwoordigt de maximale kennis die men van een systeem kan hebben.
De golffunctie kan met behulp van de Schrödingervergelijking
gevonden worden en op het eerste gezicht heeft deze vergelijking veel gemeen
met andere klassieke veldentheorieën. De materiegolf die wordt
toegekend aan het elektron ontwikkelt zich in ruimte en tijd op dezelfde
causale manier als een elektromagnetisch veld en de golfvergelijking
maakt het mogelijk om toekomstige waarden op elk punt in de
ruimte te voorspellen wanneer het veld op dit moment bekend is.
Er zijn echter enkele belangrijke verschillen. Zo blijkt dat
de golffunctie in veel gevallen niet reëel, maar noodzakelijkwijs
complex is. Verder hebben we gezien, onder andere in
vergelijking (414), dat golffunctie van een 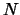 -deeltjes
systeem beschreven wordt in een
-deeltjes
systeem beschreven wordt in een 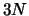 -dimensionale ruimte, terwijl
dit niet zo is voor elektromagnetische of gravitatievelden.
Dit maakt het onwaarschijnlijk dat de golffunctie van
bijvoorbeeld een elektron een meetbaar fysisch object kan zijn.
De statistische interpretatie van Born zegt dat het kwadraat
van de amplitude van de golffunctie de waarschijnlijkheidsverdeling
van het elektron voorstelt. Dit betekent dat de baan van het elektron
niet langer exact voorspelbaar is, maar enkel de waarschijnlijkheid
het elektron ergens aan te treffen. We kunnen enkel een uitspraak met
zekerheid doen voor een collectie van een groot aantal elektronen.
We zien een drastische afwijking van het klassieke idee van
determinisme en dat wordt ons opgedrongen om de twee verschijningsvormen
van het elektron - golf en deeltje - te kunnen verenigen.
-dimensionale ruimte, terwijl
dit niet zo is voor elektromagnetische of gravitatievelden.
Dit maakt het onwaarschijnlijk dat de golffunctie van
bijvoorbeeld een elektron een meetbaar fysisch object kan zijn.
De statistische interpretatie van Born zegt dat het kwadraat
van de amplitude van de golffunctie de waarschijnlijkheidsverdeling
van het elektron voorstelt. Dit betekent dat de baan van het elektron
niet langer exact voorspelbaar is, maar enkel de waarschijnlijkheid
het elektron ergens aan te treffen. We kunnen enkel een uitspraak met
zekerheid doen voor een collectie van een groot aantal elektronen.
We zien een drastische afwijking van het klassieke idee van
determinisme en dat wordt ons opgedrongen om de twee verschijningsvormen
van het elektron - golf en deeltje - te kunnen verenigen.
Stel we hebben een atoom dat zich op tijdstip 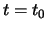 in een
aangeslagen toestand bevindt. Als we de Schrödingervergelijking
oplossen, dan vinden we dat de golffunctie geleidelijk
in de tijd evolueert van die van de aangeslagen toestand
naar die van de grondtoestand. Hiermee kunnen we op elk tijdstip
voorspellen wat de kans is het atoom aan te treffen in de
aangeslagen of in de grondtoestand. Voeren we echter op een
gegeven tijdstip (
in een
aangeslagen toestand bevindt. Als we de Schrödingervergelijking
oplossen, dan vinden we dat de golffunctie geleidelijk
in de tijd evolueert van die van de aangeslagen toestand
naar die van de grondtoestand. Hiermee kunnen we op elk tijdstip
voorspellen wat de kans is het atoom aan te treffen in de
aangeslagen of in de grondtoestand. Voeren we echter op een
gegeven tijdstip (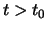 ) een meting uit aan de toestand van
het atoom, dan vinden we met een zekere waarschijnlijkheid het
atoom in de grondtoestand. Deze waarschijnlijkheid om het atoom in
de grondtoestand aan te treffen verandert continue. We dwingen een
plotselinge verandering naar zekerheid af door het uitvoeren van
een meting.
Door zijn aard en door de fysische interpretatie
(als een waarschijnlijkheidsverdeling) is het duidelijk dat de
golffunctie zelf geen fysisch object is, maar dat het ononderscheidbaar
is van het object dat bestudeerd wordt. Dit geassocieerde niet-fysische
object maakt een causale ontwikkeling door totdat er een meting
aan het object wordt uitgevoerd. Op dat moment stopt de causale
ontwikkeling en verandert haar toestand plotseling, om daarna
zich weer causaal en continue verder te ontwikkelen. Het lijkt wel
of we te maken hebben met twee verschillende aspecten van een
object: een aspect is de wereld van observaties in ruimte en tijd,
waarin de objecten die bestudeerd worden meetbare posities,
snelheden, etc. hebben. Enkel een van deze grootheden heeft een scherp
gedefinieerde waarde. Het andere aspect is de golffunctie die
geassocieerd is met het object. We kunnen deze golffunctie niet
direct met apparatuur (zintuigelijk) waarnemen. Het kan enkel
door onze geest begrepen worden en het is in die wereld waar
de ontwikkeling causaal is. Dit projecteert zich op de wereld
van gebeurtenissen in ruimte en tijd en stelt ons in staat voorspellingen
(in sommige gevallen zelfs exacte voorspellingen) te doen van resultaten
van metingen, die we kiezen om uit te voeren. Zo zijn er voor
positie en impuls twee verschillende projecties van een en dezelfde
werkelijkheid, die beide niet onderscheidbaar zijn en die beide
slechts samen een complete beschrijving van het fysische object geven.
De relatie die bestaat tussen positie en snelheid en tussen de causale
ontwikkeling van de golffuncties en de observaties, namelijk dat
ze elkaar uitsluiten, is karakteristiek voor quantummechanica en
werd door Bohr complementariteit genoemd.
) een meting uit aan de toestand van
het atoom, dan vinden we met een zekere waarschijnlijkheid het
atoom in de grondtoestand. Deze waarschijnlijkheid om het atoom in
de grondtoestand aan te treffen verandert continue. We dwingen een
plotselinge verandering naar zekerheid af door het uitvoeren van
een meting.
Door zijn aard en door de fysische interpretatie
(als een waarschijnlijkheidsverdeling) is het duidelijk dat de
golffunctie zelf geen fysisch object is, maar dat het ononderscheidbaar
is van het object dat bestudeerd wordt. Dit geassocieerde niet-fysische
object maakt een causale ontwikkeling door totdat er een meting
aan het object wordt uitgevoerd. Op dat moment stopt de causale
ontwikkeling en verandert haar toestand plotseling, om daarna
zich weer causaal en continue verder te ontwikkelen. Het lijkt wel
of we te maken hebben met twee verschillende aspecten van een
object: een aspect is de wereld van observaties in ruimte en tijd,
waarin de objecten die bestudeerd worden meetbare posities,
snelheden, etc. hebben. Enkel een van deze grootheden heeft een scherp
gedefinieerde waarde. Het andere aspect is de golffunctie die
geassocieerd is met het object. We kunnen deze golffunctie niet
direct met apparatuur (zintuigelijk) waarnemen. Het kan enkel
door onze geest begrepen worden en het is in die wereld waar
de ontwikkeling causaal is. Dit projecteert zich op de wereld
van gebeurtenissen in ruimte en tijd en stelt ons in staat voorspellingen
(in sommige gevallen zelfs exacte voorspellingen) te doen van resultaten
van metingen, die we kiezen om uit te voeren. Zo zijn er voor
positie en impuls twee verschillende projecties van een en dezelfde
werkelijkheid, die beide niet onderscheidbaar zijn en die beide
slechts samen een complete beschrijving van het fysische object geven.
De relatie die bestaat tussen positie en snelheid en tussen de causale
ontwikkeling van de golffuncties en de observaties, namelijk dat
ze elkaar uitsluiten, is karakteristiek voor quantummechanica en
werd door Bohr complementariteit genoemd.




Next: Quantummechanica en leven
Up: Klassieke fysica en werkelijkheid
Previous: Klassieke fysica en werkelijkheid
Contents
Jo van den Brand
2004-09-25