



Next: Quantummechanica en de toestand
Up: ASPECTEN VAN DE INTERPRETATIE
Previous: Consequenties van de meting
Contents
Klassieke fysica is een ontwikkeling die ongeveer driehonderd jaar
geduurd heeft en die begonnen is door Galileo, Newton en anderen.
In de mechanica van Newton kan materie worden voorgesteld als een
agregaat van massapunten, waarbij de toestand van elk massapunt
wordt gespecificeerd door middel van zes getallen: drie coordinaten
en drie snelheden. In de klassieke zienswijze heeft een deeltje
een positie en snelheid en zijn deze eigenschappen reëel en
definieren de toestand van het deeltje.
Als de toestand bekend is op enig tijdstip, dan
kunnen alle toestanden in zowel de toekomst als het verleden
berekend worden uit de bewegingswetten (bijvoorbeeld
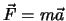 ).
Het bouwwerk was compleet met het werk over elektromagnetisme
van Maxwell, de optica van Hertz en de statistische mechanica
van Boltzmann. Al deze theorieën hebben globaal dezelfde logische
structuur: er is een objectieve werkelijkheid, onafhankelijk van
ons - de waarnemers -, die we door onze zintuigen kunnen waarnemen.
De gebeurtenissen in deze wereld volgen een strikte causale
ontwikkeling, bepaald door strikte wetten in ruimte en tijd.
De ruimte en tijd waarin deze gebeurtenissen plaatsvinden zijn de
absolute ruimte en tijd van Newton en identiek aan wat we gewend zijn
in het dagelijkse leven.
Met causale ontwikkeling bedoelen we: stel dat we op een gegeven
tijdstip complete kennis hebben van de toestand van een fysisch object
(bijvoorbeeld een deeltje of een
elektromagnetisch veld), dan kan de toekomstige
ontwikkeling van dat object (maar ook de ontwikkeling terug in de tijd)
met mathematische precisie uit de natuurwetten afgeleid worden en is
exact voorspelbaar.
).
Het bouwwerk was compleet met het werk over elektromagnetisme
van Maxwell, de optica van Hertz en de statistische mechanica
van Boltzmann. Al deze theorieën hebben globaal dezelfde logische
structuur: er is een objectieve werkelijkheid, onafhankelijk van
ons - de waarnemers -, die we door onze zintuigen kunnen waarnemen.
De gebeurtenissen in deze wereld volgen een strikte causale
ontwikkeling, bepaald door strikte wetten in ruimte en tijd.
De ruimte en tijd waarin deze gebeurtenissen plaatsvinden zijn de
absolute ruimte en tijd van Newton en identiek aan wat we gewend zijn
in het dagelijkse leven.
Met causale ontwikkeling bedoelen we: stel dat we op een gegeven
tijdstip complete kennis hebben van de toestand van een fysisch object
(bijvoorbeeld een deeltje of een
elektromagnetisch veld), dan kan de toekomstige
ontwikkeling van dat object (maar ook de ontwikkeling terug in de tijd)
met mathematische precisie uit de natuurwetten afgeleid worden en is
exact voorspelbaar.
Het was Einstein die in 1905 een ontwikkeling op gang bracht die
afweek van de logische structuur van de klassieke fysica.
Teneinde het foto-elektrisch effect te verklaren nam hij aan
dat licht bestaat uit quanta en dat deze deeltjes (fotonen) elk een
energie 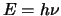 , als ook een aantal andere eigenschappen van
materiële deeltjes bezitten. Dit beeld van discontinue emissie-
en absorptieprocessen, alsook een discontinue verandering in het
aantal fotonen, staat op gespannen voet met de klassieke theorie.
Het is correct dat dergelijke discrete gebeurtenissen niet direct in
strijd met de klassieke fysica hoeven te zijn. Echter, dan nemen we aan
dat deze gebeurtenissen worden veroorzaakt door een bepaalde invloed,
en als we deze oorzaak kennen, dan kunnen we bijvoorbeeld weer exact
voorspellen op welk tijdstip de emissie van een foton zal plaatsvinden.
Met de ontwikkeling van het atoommodel van Bohr in 1913
werd het echter snel duidelijk dat het exacte tijdstip van
dergelijke emissies niet voorspelbaar is en dat deze ook niet worden
veroorzaakt door een invloed van buiten.
Het atoommodel van Bohr gaat er van uit dat
, als ook een aantal andere eigenschappen van
materiële deeltjes bezitten. Dit beeld van discontinue emissie-
en absorptieprocessen, alsook een discontinue verandering in het
aantal fotonen, staat op gespannen voet met de klassieke theorie.
Het is correct dat dergelijke discrete gebeurtenissen niet direct in
strijd met de klassieke fysica hoeven te zijn. Echter, dan nemen we aan
dat deze gebeurtenissen worden veroorzaakt door een bepaalde invloed,
en als we deze oorzaak kennen, dan kunnen we bijvoorbeeld weer exact
voorspellen op welk tijdstip de emissie van een foton zal plaatsvinden.
Met de ontwikkeling van het atoommodel van Bohr in 1913
werd het echter snel duidelijk dat het exacte tijdstip van
dergelijke emissies niet voorspelbaar is en dat deze ook niet worden
veroorzaakt door een invloed van buiten.
Het atoommodel van Bohr gaat er van uit dat
Uit de analyse van de straling van een zwart lichaam volgt dat
emissie en absorptie spontaan optreden. Verder kwam men tot
de conclusie dat wanneer atomen in een aangeslagen toestand met
energie 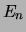 komen, de verblijftijden in deze toestand een
waarschijnlijkheidsverdeling volgen.
Enkel de gemiddelde verblijftijd, gemeten voor
een groot aantal identieke atomen in dezelfde aangeslagen toestand, is
bepaald en is een karakteristieke eigenschap van een atoom in de
desbetreffende aangeslagen toestand.
Dit was voor het eerst in de natuurkunde dat statistische beschouwingen en
kansberekening optraden in de wetten die individuele fysische objecten
beschrijven. Voorheen werd statistiek enkel toegepast op een verzameling
van een groot aantal objecten, indien men niet geinteresseerd was in
het individuele gedrag, maar waarbij elk individueel object wel de strikte
causale wetten van de klassieke mechanica volgt.
Op basis van klassieke fysica is het onmogelijk
te begrijpen dat in de laagste toestand
van een atoom een elektron eeuwig kan rondcirkelen om een kern zonder
elektromagnetische straling
uit te zenden. Verder kan men op basis van de klassieke fysica
niet de aard van de quantumsprongen in een dergelijk systeem begrijpen.
Ook de analyse van het statistische gedrag en de onvoorspelbaarheid
van bijvoorbeeld het radioactieve verval van deeltjes laat geen twijfel
bestaan over de realiteit van de intrinsieke onvoorspelbaarheid van de natuur.
komen, de verblijftijden in deze toestand een
waarschijnlijkheidsverdeling volgen.
Enkel de gemiddelde verblijftijd, gemeten voor
een groot aantal identieke atomen in dezelfde aangeslagen toestand, is
bepaald en is een karakteristieke eigenschap van een atoom in de
desbetreffende aangeslagen toestand.
Dit was voor het eerst in de natuurkunde dat statistische beschouwingen en
kansberekening optraden in de wetten die individuele fysische objecten
beschrijven. Voorheen werd statistiek enkel toegepast op een verzameling
van een groot aantal objecten, indien men niet geinteresseerd was in
het individuele gedrag, maar waarbij elk individueel object wel de strikte
causale wetten van de klassieke mechanica volgt.
Op basis van klassieke fysica is het onmogelijk
te begrijpen dat in de laagste toestand
van een atoom een elektron eeuwig kan rondcirkelen om een kern zonder
elektromagnetische straling
uit te zenden. Verder kan men op basis van de klassieke fysica
niet de aard van de quantumsprongen in een dergelijk systeem begrijpen.
Ook de analyse van het statistische gedrag en de onvoorspelbaarheid
van bijvoorbeeld het radioactieve verval van deeltjes laat geen twijfel
bestaan over de realiteit van de intrinsieke onvoorspelbaarheid van de natuur.
Soms wordt het argument gebruikt dat klassieke mechanica een complete
theorie is, in de zin dat geen onbekend mechanisme buiten beschouwing
wordt gelaten. Het is echter zo dat quantummechanica de
klassieke mechanica bevat als een speciaal geval. Als we het
gedrag van deeltjes beschouwen met toenemende massa, dan zullen volgens
de wetten van de quantummechanica, vanwege de `kleinheid' van de
constante van Planck, alle waarschijnlijkheidsverdelingen contraheren
tot bijna zekerheden. Het wordt dan mogelijk om bijna scherpe waarden
toe te kennen aan positie en snelheid en het gedrag van dergelijke
deeltjes wordt praktisch deterministisch. Aangezien quantummechanica
dus in deze limiet een deterministische theorie wordt, en de klassieke
mechanica als speciaal geval bevat, is het moeilijk zich voor te stellen dat
quantummechanica geen complete theorie zou zijn.
Subsections




Next: Quantummechanica en de toestand
Up: ASPECTEN VAN DE INTERPRETATIE
Previous: Consequenties van de meting
Contents
Jo van den Brand
2004-09-25