



Next: Meting in een willekeurige
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Verwachtingswaarden
Contents
In het volgende lopen we in gedachten het meetproces
door aan een quantummechanisch systeem met een spin-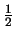 deeltje. Het idee is om in concrete termen kennis te maken
met enkele van de abstracte concepten in de theorie. We beginnen
met een deeltje in de toestand
deeltje. Het idee is om in concrete termen kennis te maken
met enkele van de abstracte concepten in de theorie. We beginnen
met een deeltje in de toestand 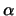 . Het deeltje bevindt zich
dus in een `spin-up' toestand. Als iemand ons zou vragen: "Wat is
de
. Het deeltje bevindt zich
dus in een `spin-up' toestand. Als iemand ons zou vragen: "Wat is
de 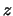 -component van het spinimpulsmoment van het deeltje?", dan
kunnen we zonder te aarzelen antwoorden:
-component van het spinimpulsmoment van het deeltje?", dan
kunnen we zonder te aarzelen antwoorden: 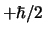 . We weten
zeker dat een meting van
. We weten
zeker dat een meting van 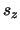 met zekerheid deze waarde zal
opleveren. Maar stel nu dat onze classicus in plaats daarvan
vraagt, "Wat is de
met zekerheid deze waarde zal
opleveren. Maar stel nu dat onze classicus in plaats daarvan
vraagt, "Wat is de  -component van het spinimpulsmoment van
dat deeltje?" We zijn verplicht te antwoorden: als je
-component van het spinimpulsmoment van
dat deeltje?" We zijn verplicht te antwoorden: als je 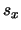 meet, heb je een kans van 50-50 procent om of
meet, heb je een kans van 50-50 procent om of 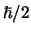 , om of
, om of
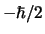 te vinden. Als onze ondervrager een klassiek fysicus
of een zogenaamde `realist' is, dan zal hij dit niet als een
bevredigend antwoord beschouwen. Je kunt dan een reactie krijgen
als, "Probeer je me nu te vertellen dat je niet weet wat
de echte toestand van het deeltje is?". In tegendeel, ik weet
precies wat de toestand van het deeltje is, namelijk
te vinden. Als onze ondervrager een klassiek fysicus
of een zogenaamde `realist' is, dan zal hij dit niet als een
bevredigend antwoord beschouwen. Je kunt dan een reactie krijgen
als, "Probeer je me nu te vertellen dat je niet weet wat
de echte toestand van het deeltje is?". In tegendeel, ik weet
precies wat de toestand van het deeltje is, namelijk
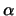 . "Maar hoe kan het dan, dat je me niet kunt vertellen
wat de
. "Maar hoe kan het dan, dat je me niet kunt vertellen
wat de  -component van de spin is?" Omdat het eenvoudig
nog geen bepaalde
-component van de spin is?" Omdat het eenvoudig
nog geen bepaalde  -component heeft. Dat kan ook niet zo
zijn, want als zowel
-component heeft. Dat kan ook niet zo
zijn, want als zowel 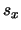 als
als 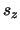 precies bekend zijn, dan
zou de onzekerheidsrelatie (572) geschonden zijn.
precies bekend zijn, dan
zou de onzekerheidsrelatie (572) geschonden zijn.
Op dit punt aangeland is onze uitdager het beu en grijpt de
apparatuur en meet de  -component van de spin. Stel
je nu voor dat hij de waarde
-component van de spin. Stel
je nu voor dat hij de waarde 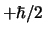 meet. "Ha!", roept
hij triomfantelijk uit, "Je hebt gelogen!". Dit deeltje heeft
een precies bepaalde waarde voor
meet. "Ha!", roept
hij triomfantelijk uit, "Je hebt gelogen!". Dit deeltje heeft
een precies bepaalde waarde voor 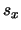 , het is
, het is 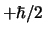 ."
Jazeker, dat heeft het nu, maar dat bewijst nog niet dat
het deze waarde had, voordat jij je meting uitvoerde.
"Je begint nu duidelijk te zeuren. Wat is er trouwens met je
onzekerheidsrelatie gebeurd? Ik weet nu zowel
."
Jazeker, dat heeft het nu, maar dat bewijst nog niet dat
het deze waarde had, voordat jij je meting uitvoerde.
"Je begint nu duidelijk te zeuren. Wat is er trouwens met je
onzekerheidsrelatie gebeurd? Ik weet nu zowel 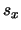 als
als 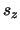 ."
Het spijt me, maar dat weet je niet: gedurende je
meting, heb je de toestand van het deeltje veranderd. Het is
nu in de toestand
."
Het spijt me, maar dat weet je niet: gedurende je
meting, heb je de toestand van het deeltje veranderd. Het is
nu in de toestand 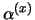 . Je weet nu wel de waarde van
. Je weet nu wel de waarde van
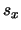 , maar je weet de waarde van
, maar je weet de waarde van 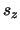 niet meer. "Nee hoor,
ik was uitermate voorzichtig om het deeltje niet te verstoren
toen ik
niet meer. "Nee hoor,
ik was uitermate voorzichtig om het deeltje niet te verstoren
toen ik 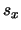 aan het meten was." Goed dan, je gelooft me niet.
Waarom controleer je het niet: meet
aan het meten was." Goed dan, je gelooft me niet.
Waarom controleer je het niet: meet 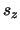 en zie wat je krijgt.
(hij kan nu natuurlijk
en zie wat je krijgt.
(hij kan nu natuurlijk 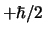 vinden en dan staan we echt
voor schut - maar als we dit hele scenario blijven herhalen,
dan zal hij in de helft van de gevallen
vinden en dan staan we echt
voor schut - maar als we dit hele scenario blijven herhalen,
dan zal hij in de helft van de gevallen 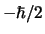 vinden).
vinden).
Voor een gewone man, een filosoof, of een klassiek fysicus,
zal een uitspraak als "dit deeltje heeft geen precies
gedefinieerde positie" (of impuls, of  -xomponent van het
spinimpulsmoment, of wat dan ook) vaag klinken, incompetent
zelfs. Maar het is geen van alle. Het is een direct
gevolg van de axioma's van de quantum theorie.
-xomponent van het
spinimpulsmoment, of wat dan ook) vaag klinken, incompetent
zelfs. Maar het is geen van alle. Het is een direct
gevolg van de axioma's van de quantum theorie.




Next: Meting in een willekeurige
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Verwachtingswaarden
Contents
Jo van den Brand
2004-09-25
![]() -component van de spin. Stel
je nu voor dat hij de waarde
-component van de spin. Stel
je nu voor dat hij de waarde ![]() meet. "Ha!", roept
hij triomfantelijk uit, "Je hebt gelogen!". Dit deeltje heeft
een precies bepaalde waarde voor
meet. "Ha!", roept
hij triomfantelijk uit, "Je hebt gelogen!". Dit deeltje heeft
een precies bepaalde waarde voor ![]() , het is
, het is ![]() ."
Jazeker, dat heeft het nu, maar dat bewijst nog niet dat
het deze waarde had, voordat jij je meting uitvoerde.
"Je begint nu duidelijk te zeuren. Wat is er trouwens met je
onzekerheidsrelatie gebeurd? Ik weet nu zowel
."
Jazeker, dat heeft het nu, maar dat bewijst nog niet dat
het deze waarde had, voordat jij je meting uitvoerde.
"Je begint nu duidelijk te zeuren. Wat is er trouwens met je
onzekerheidsrelatie gebeurd? Ik weet nu zowel ![]() als
als ![]() ."
Het spijt me, maar dat weet je niet: gedurende je
meting, heb je de toestand van het deeltje veranderd. Het is
nu in de toestand
."
Het spijt me, maar dat weet je niet: gedurende je
meting, heb je de toestand van het deeltje veranderd. Het is
nu in de toestand ![]() . Je weet nu wel de waarde van
. Je weet nu wel de waarde van
![]() , maar je weet de waarde van
, maar je weet de waarde van ![]() niet meer. "Nee hoor,
ik was uitermate voorzichtig om het deeltje niet te verstoren
toen ik
niet meer. "Nee hoor,
ik was uitermate voorzichtig om het deeltje niet te verstoren
toen ik ![]() aan het meten was." Goed dan, je gelooft me niet.
Waarom controleer je het niet: meet
aan het meten was." Goed dan, je gelooft me niet.
Waarom controleer je het niet: meet ![]() en zie wat je krijgt.
(hij kan nu natuurlijk
en zie wat je krijgt.
(hij kan nu natuurlijk ![]() vinden en dan staan we echt
voor schut - maar als we dit hele scenario blijven herhalen,
dan zal hij in de helft van de gevallen
vinden en dan staan we echt
voor schut - maar als we dit hele scenario blijven herhalen,
dan zal hij in de helft van de gevallen ![]() vinden).
vinden).
![]() -xomponent van het
spinimpulsmoment, of wat dan ook) vaag klinken, incompetent
zelfs. Maar het is geen van alle. Het is een direct
gevolg van de axioma's van de quantum theorie.
-xomponent van het
spinimpulsmoment, of wat dan ook) vaag klinken, incompetent
zelfs. Maar het is geen van alle. Het is een direct
gevolg van de axioma's van de quantum theorie.