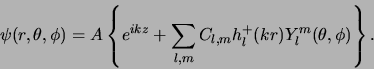Next: Deeltje in de Coulomb
Up: WATERSTOFATOOM
Previous: Algemene oplossing oneindige potentiaal
Contents
We beschouwen hier de quantummechanische beschrijving van
de botsing van twee deeltjes, of beter gezegd, de verstrooiing
van een inkomende vlakke golf, 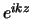 , aan een sferisch symmetrische
potentiaal,
, aan een sferisch symmetrische
potentiaal, 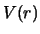 . Het verstrooiingsproces wordt weergegeven
in figuur 35.
. Het verstrooiingsproces wordt weergegeven
in figuur 35.
Figuur 35:
Verstrooiing van golven, waarbij een inkomende golf een
uitgaande sferische golf genereert.
|
|
We hebben te maken met een inkomende vlakke golf,
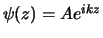 ,
die in de
,
die in de 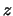 -richting beweegt. De golf komt een verstrooiingspotentiaal
tegen en genereert een uitgaande sferische golf. We zoeken dus oplossingen
van de Schrödingervergelijking van de vorm
-richting beweegt. De golf komt een verstrooiingspotentiaal
tegen en genereert een uitgaande sferische golf. We zoeken dus oplossingen
van de Schrödingervergelijking van de vorm
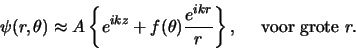 |
(467) |
De sferische golf dient af te vallen met 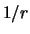 , omdat dit deel
van
, omdat dit deel
van
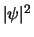 met
met 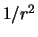 moet gaan om waarschijnlijkheid
te behouden. We noemen
moet gaan om waarschijnlijkheid
te behouden. We noemen 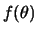 de verstrooiingsamplitude.
de verstrooiingsamplitude.
We zoeken oplossingen van de vorm
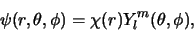 |
(468) |
met 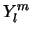 de sferisch harmonischen en
de sferisch harmonischen en
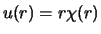 .
Deze laatste moet een oplossing zijn van de radiële vergelijking
.
Deze laatste moet een oplossing zijn van de radiële vergelijking
![\begin{displaymath}
-{\hbar^2 \over 2m}{d^2 u \over dr^2} + \left[ V(r) +
{\hbar^2 \over 2m} {l(l+1) \over r^2} \right] u = Eu.
\end{displaymath}](img1411.png) |
(469) |
Op grote afstand (
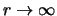 ) gaat de potentiaal
naar nul en is ook de centrifugale term verwaarloosbaar. We hebben dan
) gaat de potentiaal
naar nul en is ook de centrifugale term verwaarloosbaar. We hebben dan
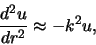 |
(470) |
met
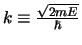 . De algemene oplossing is dan
. De algemene oplossing is dan
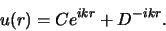 |
(471) |
De eerste term vertegenwoordigt een uitgaande sferische golf en de
tweede een inkomende sferische golf - in ons geval willen we 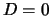 .
Op grote afstand vinden we dus
.
Op grote afstand vinden we dus
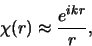 |
(472) |
zoals we in de inleiding al aangaven.
Als we aannemen dat de potentiaal lokaal is, dan is er een gebied
waarvoor de potentiaal 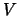 verwaarloosd kan worden, maar waar we
rekening moeten houden met de centrifugale term. In dit intermediaire
gebied kunnen we de radiële vergelijking schrijven als
verwaarloosd kan worden, maar waar we
rekening moeten houden met de centrifugale term. In dit intermediaire
gebied kunnen we de radiële vergelijking schrijven als
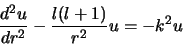 |
(473) |
en de algemene oplossing hiervan hebben we reeds in de vorige paragraaf
gevonden. Het is een lineaire combinatie van sferische Bessel
en Neumann functies,
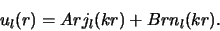 |
(474) |
Het is echter zo, dat zowel 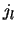 (iets als een sin-functie)
als
(iets als een sin-functie)
als 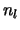 (iets als een cos-functie) geen uitgaande (of inkomende)
golf kan voorstellen. We hebben een lineaire combinatie hiervan
nodig (analoog aan
(iets als een cos-functie) geen uitgaande (of inkomende)
golf kan voorstellen. We hebben een lineaire combinatie hiervan
nodig (analoog aan 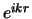 en
en 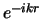 ). Deze combinatie
staat bekend als de sferische Hankel functies en is
gedefineerd als
). Deze combinatie
staat bekend als de sferische Hankel functies en is
gedefineerd als
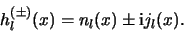 |
(475) |
Merk op dat
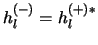 .
.
De laagste-orde Hankel functies zijn
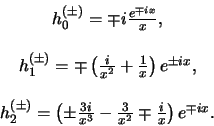 |
(476) |
We zien dat de Hankel functie van de eerste soort, 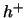 ,
als
,
als 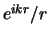 gaat, terwijl de Hankel functie van de tweede soort,
gaat, terwijl de Hankel functie van de tweede soort,
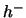 als
als 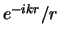 gaat. Voor uitgaande sferische golven hebben
we duidelijk de sferische Hankel functie van de eerste soort nodig.
gaat. Voor uitgaande sferische golven hebben
we duidelijk de sferische Hankel functie van de eerste soort nodig.
Hierbij schrijven we voor de complete golffunctie,
in het externe gebied met 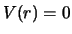 ,
,
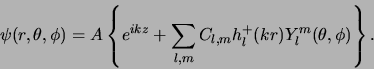 |
(477) |
Tenslotte merken we op dat we nu ook een vergelijking kunnen vinden
voor de golffunctie van een vrij deeltje uitgedrukt in
sferische coördinaten. Er geldt onderstaande expansie van een
vlakke golf
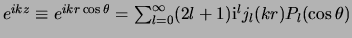 . . |
| |




Next: Deeltje in de Coulomb
Up: WATERSTOFATOOM
Previous: Algemene oplossing oneindige potentiaal
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=12cm]{Figures/scatter.eps}](img1401.png)
![\includegraphics[width=12cm]{Figures/scatter.eps}](img1401.png)
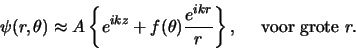
![\begin{displaymath}
-{\hbar^2 \over 2m}{d^2 u \over dr^2} + \left[ V(r) +
{\hbar^2 \over 2m} {l(l+1) \over r^2} \right] u = Eu.
\end{displaymath}](img1411.png)
![]() verwaarloosd kan worden, maar waar we
rekening moeten houden met de centrifugale term. In dit intermediaire
gebied kunnen we de radiële vergelijking schrijven als
verwaarloosd kan worden, maar waar we
rekening moeten houden met de centrifugale term. In dit intermediaire
gebied kunnen we de radiële vergelijking schrijven als
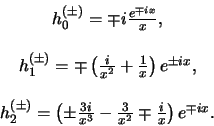
![]() ,
,