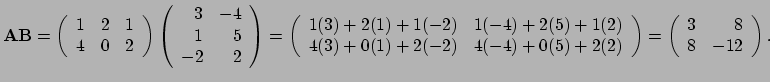Next: Diagonale matrices
Up: Matrixrekening
Previous: Product van scalar met
Contents
Definitie: Het product
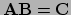 van de matrix
van de matrix
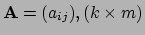 met de matrix
met de matrix
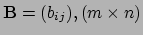 , is de matrix
, is de matrix
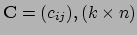 , waarvan
, waarvan
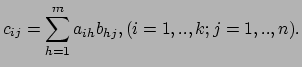 |
(452) |
Het element 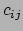 van
van 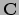 is dus gelijk aan het inwendig
product van de
is dus gelijk aan het inwendig
product van de 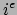 rijvector van
rijvector van 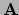 met de
met de 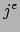 kolomvector
van
kolomvector
van 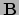 .
.
Voorbeeld: Als
en
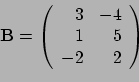 , dan
, dan
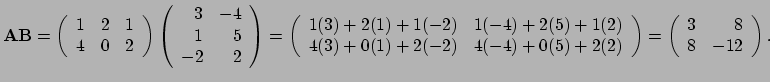 |
(453) |
Opmerkingen
- De vermenigvuldiging van een matrix met een kolomvector is
een bijzonder geval van deze matrixvermenigvuldiging: een kolomvector
is immers een matrix van de orde
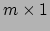 .
.
- Het product
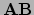 bestaat slechts dan als het aantal
kolommen van
bestaat slechts dan als het aantal
kolommen van 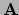 gelijk is aan het aantal rijen van
gelijk is aan het aantal rijen van 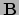 .
.
Matrix vermenigvuldiging is in het algemeen niet commutatief,
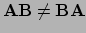 . Het verschil tussen deze twee volgordes noemen
we de commutator,
. Het verschil tussen deze twee volgordes noemen
we de commutator,
![$\displaystyle [ {\bf A}, {\bf B} ] \equiv {\bf AB} - {\bf BA} .$](img2007.png) |
(454) |
Tenslotte merken we op dat matrixvermenigvuldiging wel associatief is
(
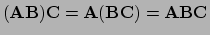 )
en distributief (
)
en distributief (
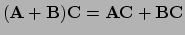 en
en
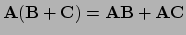 ).
).




Next: Diagonale matrices
Up: Matrixrekening
Previous: Product van scalar met
Contents
Jo van den Brand
2009-01-31
![]() van de matrix
van de matrix
![]() met de matrix
met de matrix
![]() , is de matrix
, is de matrix
![]() , waarvan
, waarvan
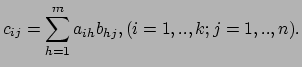
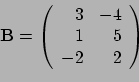 , dan
, dan