



Next: Kosmische straling
Up: Quantumfysische verschijnselen in het
Previous: Neutrino astronomie
Contents
We beperken de discussie tot twee flavors, het elektron neutrino 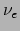 en het muon neutrino
en het muon neutrino 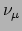 . De flavor eigentoestanden,
. De flavor eigentoestanden, 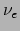 en
en 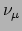 ,
zijn echter geen massa eigentoestanden,
,
zijn echter geen massa eigentoestanden, 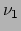 en
en 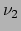 ,
maar zijn hieraan gerelateerd door een zogenaamde menghoek
,
maar zijn hieraan gerelateerd door een zogenaamde menghoek 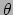 ,
,
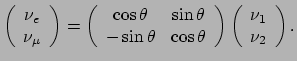 |
(69) |
We nemen aan dat we een bundel 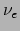 's geproduceerd hebben met een precieze
impuls, waarbij alle deeltjes in de
's geproduceerd hebben met een precieze
impuls, waarbij alle deeltjes in de 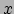 -richting bewegen en de bron zich
op
-richting bewegen en de bron zich
op 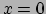 bevindt. We vragen ons af wat de waarschijnlijkheid is om een
bevindt. We vragen ons af wat de waarschijnlijkheid is om een 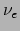 te detecteren op positie
te detecteren op positie 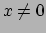 ?
?
Neem aan dat we op tijdstip 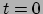 een zuivere
een zuivere 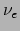 toestand hebben.
Omdat
toestand hebben.
Omdat 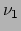 en
en 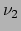 massa eigentoestanden zijn, en omdat de bundel bestaat
uit eigentoestanden van impuls, vertelt de relatie
massa eigentoestanden zijn, en omdat de bundel bestaat
uit eigentoestanden van impuls, vertelt de relatie
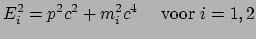 |
(70) |
ons, dat dit ook eigentoestanden van energie zijn. De tijdevolutie wordt daarom
gegeven door de uitdrukkingen
Vervolgens gebruiken we de gegeven relatie tussen  en
en  en vinden
dat de golffunctie op
en vinden
dat de golffunctie op 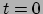 geschreven kan worden als
geschreven kan worden als
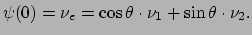 |
(71) |
We gebruiken de tijdafhankelijkheid van de 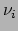 en kunnen de
volledige oplossing van de Schrödingervergelijking met als begintoestand
en kunnen de
volledige oplossing van de Schrödingervergelijking met als begintoestand
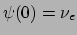 schrijven als
schrijven als
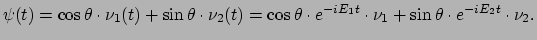 |
(72) |
De waarschijnlijkheid om een 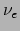 te detecteren is het kwadraat van de
projectie van
te detecteren is het kwadraat van de
projectie van 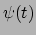 op de flavoreigentoestand
op de flavoreigentoestand 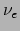 . We maken
gebruik van de orthonormaliteitsrelaties voor de massa eigentoestanden,
. We maken
gebruik van de orthonormaliteitsrelaties voor de massa eigentoestanden,
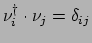 |
(73) |
en berekenen de projectie als
Als we het kwadraat nemen van bovenstaande uidrukking vinden we
We zien dat de periode van oscillatie gegeven wordt door
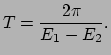 |
(75) |
Als we aannemen dat de neutrino's ultra-relativistisch zijn, dus
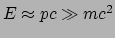 , dan geldt
, dan geldt
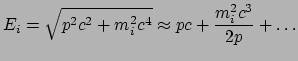 |
(76) |
Als we dit invullen vinden we
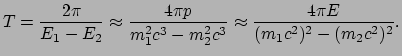 |
(77) |
Omdat de neutrino's ultra-relativistisch bewegen, bewegen ze zich met
praktisch de lichtsnelheid. De afgelegde weg bedraagt dus
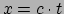 .
We zien dat de flavor oscillatie in de tijd, zich vertaalt in een oscillatie
van de neutrino flavor als functie van de afstand tot de bron. De afstand
die correspondeert met een oscillatieperiode wordt de oscillatielengte,
.
We zien dat de flavor oscillatie in de tijd, zich vertaalt in een oscillatie
van de neutrino flavor als functie van de afstand tot de bron. De afstand
die correspondeert met een oscillatieperiode wordt de oscillatielengte,
 , genoemd. We vinden hiermee de relatie
, genoemd. We vinden hiermee de relatie
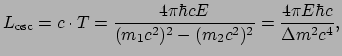 |
(78) |
met
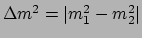 . Als we de juiste
conversiefactoren gebruiken vinden we
. Als we de juiste
conversiefactoren gebruiken vinden we
Figuur 20:
Gebieden in de neutrino parameterruimte opgespannen
door
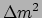 en menghoek
en menghoek 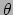 die worden uitgesloten of
die waarvoor er een voorkeur voor de waarden van deze parameters bestaat.
die worden uitgesloten of
die waarvoor er een voorkeur voor de waarden van deze parameters bestaat.
|
|
Er zijn diverse experimenten uitgevoerd om neutrino oscillaties te
observeren. Hierbij werden neutrino's van zowel de zon, als
kernreactoren alsook de neutrino's geproduceerd in atmosferische
showers van kosmische straling gebruikt. Fig. 20
toont de gebieden in de neutrino parameterruimte opgespannen
door
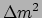 en menghoek
en menghoek 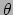 die worden uitgesloten of
die waarvoor er een voorkeur bestaat. De huidige consensus is
dat neutrino oscillaties zijn waargenomen met een significantie
van ongeveer 5
die worden uitgesloten of
die waarvoor er een voorkeur bestaat. De huidige consensus is
dat neutrino oscillaties zijn waargenomen met een significantie
van ongeveer 5 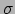 .
.




Next: Kosmische straling
Up: Quantumfysische verschijnselen in het
Previous: Neutrino astronomie
Contents
Jo van den Brand
2009-01-31
![]() en het muon neutrino
en het muon neutrino ![]() . De flavor eigentoestanden,
. De flavor eigentoestanden, ![]() en
en ![]() ,
zijn echter geen massa eigentoestanden,
,
zijn echter geen massa eigentoestanden, ![]() en
en ![]() ,
maar zijn hieraan gerelateerd door een zogenaamde menghoek
,
maar zijn hieraan gerelateerd door een zogenaamde menghoek ![]() ,
,
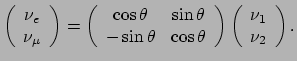
![]() een zuivere
een zuivere ![]() toestand hebben.
Omdat
toestand hebben.
Omdat ![]() en
en ![]() massa eigentoestanden zijn, en omdat de bundel bestaat
uit eigentoestanden van impuls, vertelt de relatie
massa eigentoestanden zijn, en omdat de bundel bestaat
uit eigentoestanden van impuls, vertelt de relatie
![]() te detecteren is het kwadraat van de
projectie van
te detecteren is het kwadraat van de
projectie van ![]() op de flavoreigentoestand
op de flavoreigentoestand ![]() . We maken
gebruik van de orthonormaliteitsrelaties voor de massa eigentoestanden,
. We maken
gebruik van de orthonormaliteitsrelaties voor de massa eigentoestanden,
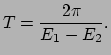
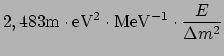
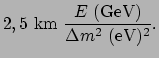
![\includegraphics[width=12cm]{Figures/neutrinomap.eps}](img543.png)
![]() en menghoek
en menghoek ![]() die worden uitgesloten of
die waarvoor er een voorkeur bestaat. De huidige consensus is
dat neutrino oscillaties zijn waargenomen met een significantie
van ongeveer 5
die worden uitgesloten of
die waarvoor er een voorkeur bestaat. De huidige consensus is
dat neutrino oscillaties zijn waargenomen met een significantie
van ongeveer 5 ![]() .
.