Next: Tijdevolutie van een Systeem
Up: Impulsmoment van een Systeem
Previous: Impulsmoment van een Systeem
De natuur realiseert de half-integer waarden voor impulsmoment
in de vorm van het intrinsieke impulsmoment in het rustsysteem van
deeltjes, zoals elektronen, protonen, neutronen, quarks, neutrino's, enz.
Conventioneel gebruikt met symbool 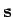 voor de operator van
dit zogenaamde spin impulsmoment, terwijl
voor de operator van
dit zogenaamde spin impulsmoment, terwijl 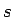 en
en 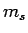 de geassocieerde spin en
magnetische quantumgetallen zijn. Er geldt dat
de geassocieerde spin en
magnetische quantumgetallen zijn. Er geldt dat
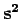 de waarde
de waarde
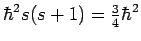 heeft. De projectie
heeft. De projectie 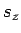 heeft slechts twee eigenwaarden
heeft slechts twee eigenwaarden 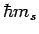 met
met
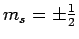 , die corresponderen met de spin parallel
(spin up:
, die corresponderen met de spin parallel
(spin up: 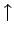 ) en spin antiparallel (spin down:
) en spin antiparallel (spin down: 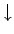 )
aan de
)
aan de 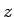 -as. De corresponderende eigentoestanden van
-as. De corresponderende eigentoestanden van 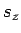 kunnen
geschreven worden als
kunnen
geschreven worden als
 |
(46) |
en dus
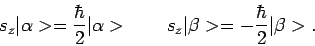 |
(47) |
Omdat de toestanden
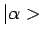 en
en 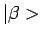 behoren
bij verschillende eigenwaarden van
behoren
bij verschillende eigenwaarden van 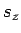 , zijn ze orthogonaal. We
nemen verder aan dat ze genormeerd zijn. Er geldt
, zijn ze orthogonaal. We
nemen verder aan dat ze genormeerd zijn. Er geldt
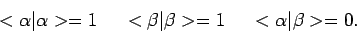 |
(48) |
Spin-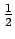 impulsmoment kan eenvoudig worden behandeld door
de spinoperatoren voor te stellen als
impulsmoment kan eenvoudig worden behandeld door
de spinoperatoren voor te stellen als 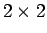 matrices en
de spintoestanden door twee-component kolomvectoren. We schrijven
matrices en
de spintoestanden door twee-component kolomvectoren. We schrijven
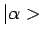 en
en 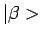 als
als
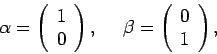 |
(49) |
en de spinimpulsmoment operatoren door
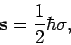 |
(50) |
waarbij
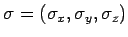 de Pauli matrices
zijn, gedefinieerd door
de Pauli matrices
zijn, gedefinieerd door
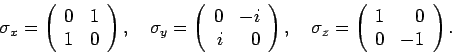 |
(51) |
Met behulp van bovenstaande relaties kunnen we direct een aantal
resultaten afleiden. Er geldt
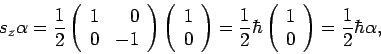 |
(52) |
hetgeen de matrixvorm is van de eerste uitdrukking in
vergelijking (47).
De spinmatrices voldoen aan de
commutatieregels voor impulsmoment,
![$\left[ s_x , s_y \right] = i \hbar s_z, ~~~{\rm enz.}$](img126.gif) ,
waarbij men gebruik dient te maken van de regels voor
matrixvermenigvuldiging1.
,
waarbij men gebruik dient te maken van de regels voor
matrixvermenigvuldiging1.
De algemene spintoestand
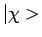 kan geschreven worden als
kan geschreven worden als
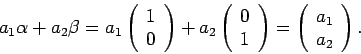 |
(54) |
Verder definieren we het scalaire product. Stel dat
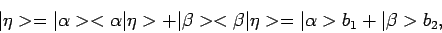 |
(55) |
dan is het scalaire product hiervan met de toestand
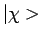 , gegeven door vergelijking (54), gelijk aan
, gegeven door vergelijking (54), gelijk aan
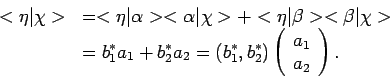 |
(56) |
Het laatste deel van deze uitdrukking is de matrixvorm van het
scalaire product. Hierbij wordt de ket 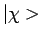 voorgesteld als
een kolomvector, terwijl de bra
voorgesteld als
een kolomvector, terwijl de bra 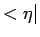 wordt voorgesteld
als een rijvector. Het scalaire product volgt uit de regels van
matrixvermenigvuldiging.
wordt voorgesteld
als een rijvector. Het scalaire product volgt uit de regels van
matrixvermenigvuldiging.
We gaan het matrixformulisme voor spin-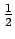 deeltjes nu
toepassen. Allereerst berekenen
we de verwachtingswaarde van
deeltjes nu
toepassen. Allereerst berekenen
we de verwachtingswaarde van 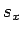 voor de spintoestand
voor de spintoestand 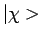 .
We vinden
.
We vinden
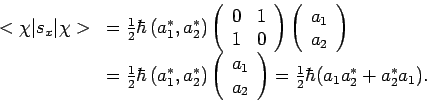 |
(57) |
Evenzo berekenen we
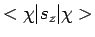 . Er geldt
. Er geldt
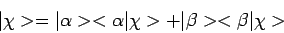 |
(58) |
en dus
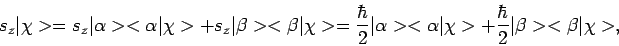 |
(59) |
waarmee we vinden
![\begin{displaymath}
< \chi \vert s_z \vert \chi >
= {\hbar \over 2} \left[ \ver...
...over 2} \left[ \vert a_1 \vert^2 - \vert a_2 \vert^2 \right] .
\end{displaymath}](img139.gif) |
(60) |
We zien dat respectievelijk
de eerste en tweede term de waarschijnlijkheid geven dat het
deeltje in de spintoestand 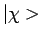 spin up of spin down heeft.
spin up of spin down heeft.
Tenslotte beschouwen we de eigenwaarden en eigenfuncties van een
component van de spinoperator 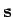 in de richting van een
eenheidsvector
in de richting van een
eenheidsvector 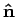 . Dit komt neer op het oplossen van de
eigenwaardenvergelijking
. Dit komt neer op het oplossen van de
eigenwaardenvergelijking
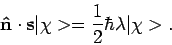 |
(61) |
Ter vereenvoudiging nemen we aan dat 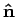 in het
in het
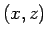 -vlak ligt en de componenten
-vlak ligt en de componenten
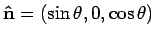 heeft, met
heeft, met
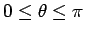 en
en
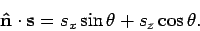 |
(62) |
Gebruik maken van de Pauli matrices levert
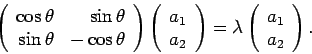 |
(63) |
Bovenstaande vergelijking kan eenvoudig worden opgelost. We
vinden de equivalente vergelijkingen
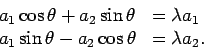 |
(64) |
Elk van deze vergelijkingen geeft een uitdrukking voor
de verhouding 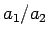 en het is eenvoudig na te gaan dat
de vergelijkingen enkel consistent zijn
als geldt dat
en het is eenvoudig na te gaan dat
de vergelijkingen enkel consistent zijn
als geldt dat
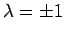 .
De eigenwaarden van
.
De eigenwaarden van
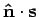 zijn dus
zijn dus
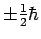 en hiermee zijn ze
hetzelfde2 als die van
en hiermee zijn ze
hetzelfde2 als die van 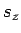 .
We vinden de relaties
.
We vinden de relaties
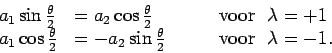 |
(65) |
De normalisatieconditie
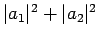 leidt
tot de genormeerde eigenvectoren
leidt
tot de genormeerde eigenvectoren
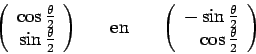 |
(66) |
voor 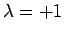 en
en 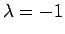 respectievelijk.
De willekeurige fasefactor in elk van deze eigenvectoren is
zodanig gekozen dat voor
respectievelijk.
De willekeurige fasefactor in elk van deze eigenvectoren is
zodanig gekozen dat voor 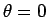 (corresponderend met
(corresponderend met
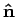 in de richting van de
in de richting van de 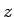 -as) de vectoren
samenvallen met de eigenvectoren
-as) de vectoren
samenvallen met de eigenvectoren 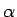 en
en 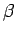 .
.
We duiden de eigenkets van
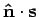 met
eigenwaarden
met
eigenwaarden
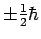 aan met
aan met
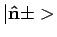 , dan vinden we
, dan vinden we
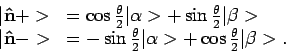 |
(67) |
Uit bovenstaande vergelijking kan men eenvoudig de waarschijnlijkheid
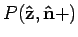 afleiden dat een meting van de
spincomponent
afleiden dat een meting van de
spincomponent
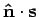 van een deeltje in de
toestand
van een deeltje in de
toestand 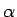 (dus met spin parallel aan de eenheidsvector
(dus met spin parallel aan de eenheidsvector
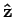 in de richting van de positieve
in de richting van de positieve 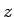 -as) het resultaat
-as) het resultaat
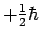 oplevert. Deze waarschijnlijkheid kan
verkregen worden door de expansie van
oplevert. Deze waarschijnlijkheid kan
verkregen worden door de expansie van
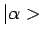 te beschouwen
in termen van de orthonormale spin eigentoestanden
te beschouwen
in termen van de orthonormale spin eigentoestanden
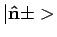 en wordt gegeven
door
en wordt gegeven
door
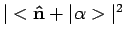 . We vinden
. We vinden
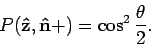 |
(68) |
Dit belangrijke resultaat zullen we nodig hebben tijdens de discussie van
de ongelijkheid van Bell.



Next: Tijdevolutie van een Systeem
Up: Impulsmoment van een Systeem
Previous: Impulsmoment van een Systeem
Jo van den Brand
2002-11-23
![]() voor de operator van
dit zogenaamde spin impulsmoment, terwijl
voor de operator van
dit zogenaamde spin impulsmoment, terwijl ![]() en
en ![]() de geassocieerde spin en
magnetische quantumgetallen zijn. Er geldt dat
de geassocieerde spin en
magnetische quantumgetallen zijn. Er geldt dat
![]() de waarde
de waarde
![]() heeft. De projectie
heeft. De projectie ![]() heeft slechts twee eigenwaarden
heeft slechts twee eigenwaarden ![]() met
met
![]() , die corresponderen met de spin parallel
(spin up:
, die corresponderen met de spin parallel
(spin up: ![]() ) en spin antiparallel (spin down:
) en spin antiparallel (spin down: ![]() )
aan de
)
aan de ![]() -as. De corresponderende eigentoestanden van
-as. De corresponderende eigentoestanden van ![]() kunnen
geschreven worden als
kunnen
geschreven worden als
![]() impulsmoment kan eenvoudig worden behandeld door
de spinoperatoren voor te stellen als
impulsmoment kan eenvoudig worden behandeld door
de spinoperatoren voor te stellen als ![]() matrices en
de spintoestanden door twee-component kolomvectoren. We schrijven
matrices en
de spintoestanden door twee-component kolomvectoren. We schrijven
![]() en
en ![]() als
als
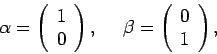
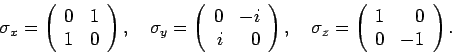
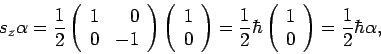
![]() kan geschreven worden als
kan geschreven worden als
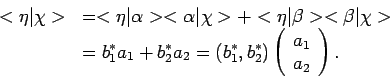
![]() deeltjes nu
toepassen. Allereerst berekenen
we de verwachtingswaarde van
deeltjes nu
toepassen. Allereerst berekenen
we de verwachtingswaarde van ![]() voor de spintoestand
voor de spintoestand ![]() .
We vinden
.
We vinden
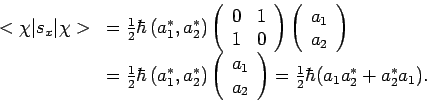
![]() in de richting van een
eenheidsvector
in de richting van een
eenheidsvector ![]() . Dit komt neer op het oplossen van de
eigenwaardenvergelijking
. Dit komt neer op het oplossen van de
eigenwaardenvergelijking
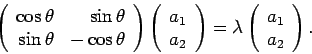

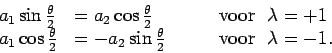
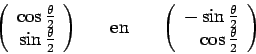
![]() met
eigenwaarden
met
eigenwaarden
![]() aan met
aan met
![]() , dan vinden we
, dan vinden we