


Next: Impulsmoment van een Systeem
Up: Aspecten van de Interpretatie
Previous: Mathematische Basis van de
In de notatie die is ingevoerd door Dirac schrijven we in plaats
van de golffuncties 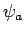 ,
, 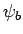 , ... de toestanden
, ... de toestanden
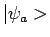 ,
,
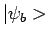 , ... of zelfs
, ... of zelfs 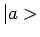 ,
,
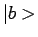 , ... waarbij
, ... waarbij 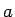 ,
, 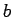 , ...de toestanden labelen waarvan
de golffuncties
, ...de toestanden labelen waarvan
de golffuncties 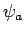 ,
, 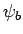 , ... zijn. Het symbool
, ... zijn. Het symbool 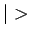 werd door Dirac een ket genoemd, terwijl de bra
werd door Dirac een ket genoemd, terwijl de bra 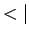 de complex geconjugeerde toestand voorstelt. In deze notatie kan het scalaire
product van twee toestanden
de complex geconjugeerde toestand voorstelt. In deze notatie kan het scalaire
product van twee toestanden 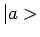 en
en 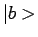 geschreven
worden als
geschreven
worden als
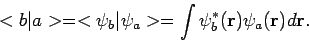 |
(22) |
Uit deze definitie kunnen de volgende eigenschappen van het
scalaire product worden afgeleid.
Een ket 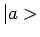 is genormeerd als
is genormeerd als
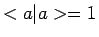 en twee
kets
en twee
kets 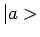 en
en 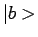 zij orthogonaal als
zij orthogonaal als
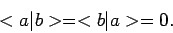 |
(28) |
Als
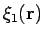 ,
,
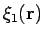 , ... een complete set
orthonormale golffuncties is, dan geldt
, ... een complete set
orthonormale golffuncties is, dan geldt
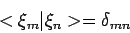 |
(29) |
en de expansie van een willekeurige golffunctie
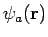 in
termen van de complete set
in
termen van de complete set
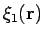 ,
,
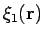 , ...
heeft in Dirac notatie de vorm
, ...
heeft in Dirac notatie de vorm
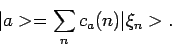 |
(30) |
Als we het scalair product hiervan nemen met 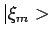 , dan verkrijgen
we de expansiecoëfficiënt
, dan verkrijgen
we de expansiecoëfficiënt
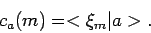 |
(31) |
en hiermee kunnen we vergelijking (30) schrijven als
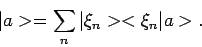 |
(32) |
In een meer eenvoudige notatie vinden we voor vergelijking (32)
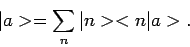 |
(33) |
We zien dat de operator
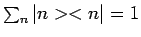 voor een complete set.
voor een complete set.
In Dirac notatie verandert een operator 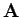 een toestand
een toestand
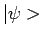 in een toestand
in een toestand 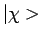 die we ook kunnen
labelen als
die we ook kunnen
labelen als
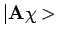 . We schrijven
. We schrijven
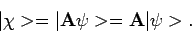 |
(34) |
Als we het scalair product nemen van vergelijking (34)
met een willekeurige ket 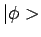 , vinden we
, vinden we
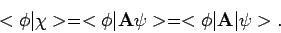 |
(35) |
Uit vergelijkingen (23) en (35) volgt dat
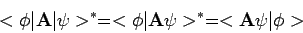 |
(36) |
We noemen
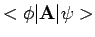 het matrixelement van de
operator
het matrixelement van de
operator 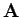 tussen de toestanden
tussen de toestanden 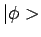 en
en 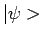 .
Voor een Hermitische operator geldt in analogie met vergelijking
(3) in Dirac notatie dat voor willekeurige toestanden
.
Voor een Hermitische operator geldt in analogie met vergelijking
(3) in Dirac notatie dat voor willekeurige toestanden
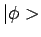 en
en 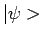 moet gelden dat
moet gelden dat
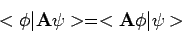 |
(37) |
Met behulp van vergelijkingen (35) en (36)
kan dit geschreven worden als
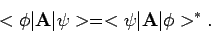 |
(38) |



Next: Impulsmoment van een Systeem
Up: Aspecten van de Interpretatie
Previous: Mathematische Basis van de
Jo van den Brand
2002-11-23
![]() ,
, ![]() , ... de toestanden
, ... de toestanden
![]() ,
,
![]() , ... of zelfs
, ... of zelfs ![]() ,
,
![]() , ... waarbij
, ... waarbij ![]() ,
, ![]() , ...de toestanden labelen waarvan
de golffuncties
, ...de toestanden labelen waarvan
de golffuncties ![]() ,
, ![]() , ... zijn. Het symbool
, ... zijn. Het symbool ![]() werd door Dirac een ket genoemd, terwijl de bra
werd door Dirac een ket genoemd, terwijl de bra ![]() de complex geconjugeerde toestand voorstelt. In deze notatie kan het scalaire
product van twee toestanden
de complex geconjugeerde toestand voorstelt. In deze notatie kan het scalaire
product van twee toestanden ![]() en
en ![]() geschreven
worden als
geschreven
worden als
![]() is genormeerd als
is genormeerd als
![]() en twee
kets
en twee
kets ![]() en
en ![]() zij orthogonaal als
zij orthogonaal als
![]() ,
,
![]() , ... een complete set
orthonormale golffuncties is, dan geldt
, ... een complete set
orthonormale golffuncties is, dan geldt
![]() een toestand
een toestand
![]() in een toestand
in een toestand ![]() die we ook kunnen
labelen als
die we ook kunnen
labelen als
![]() . We schrijven
. We schrijven