De verwachtingswaarde van de observabele ![]() voor een
systeem beschreven door toestand
voor een
systeem beschreven door toestand ![]() wordt gegeven door
wordt gegeven door
| (1) |
De conditie gegeven door vergelijking (2) voor de Hermiticiteit
van een operator is equivalent met de conditie dat voor twee
willekeurige toestanden ![]() en
en ![]() geldt dat
geldt dat
![\begin{displaymath}
\sum_{m,n=1}^2 c_m^* c_n \left[ \int \psi_m^* {\bf A} \psi_n d{\bf r} -
\int ({\bf A} \psi_m)^* \psi_n d{\bf r} \right] = 0
\end{displaymath}](img13.gif) |
(5) |
| (6) |
Vervolgens vragen we ons af of er toestanden ![]() bestaan waarvoor het
resultaat van metingen van de observabele
bestaan waarvoor het
resultaat van metingen van de observabele ![]() uniek is, dus waarbij
metingen van
uniek is, dus waarbij
metingen van ![]() altijd tot dezelfde waarde leiden. In het algemeen
weten we dat het uitvoeren van meerdere metingen aan identiek geprepareerde
systemen in de toestand
altijd tot dezelfde waarde leiden. In het algemeen
weten we dat het uitvoeren van meerdere metingen aan identiek geprepareerde
systemen in de toestand ![]() zullen leiden tot resultaten met een spreiding
zullen leiden tot resultaten met een spreiding
![]() rond de meest waarschijnlijke waarde
rond de meest waarschijnlijke waarde ![]() . Als een maat
voor de spreiding nemen we de standaarddeviatie
. Als een maat
voor de spreiding nemen we de standaarddeviatie
![]() , gedefinieerd
door
, gedefinieerd
door
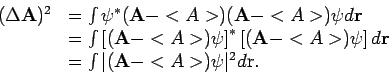 |
(7) |
| (9) |
Een fysische observable van een systeem correspondeert met een
Hermitische operator in de theorie. Deze operator heeft een spectrum
van eigenwaarden en eigenfuncties. We hebben
| (10) |
De eigenfuncties van een Hermitische operator hebben de belangrijke
eigenschap dat ze een orthonormaal stelsel vormen. Er geldt
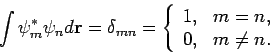 |
(11) |
Een andere belangrijke eigenschap van Hermitische operatoren is dat
de verzameling eigenfuncties,
![]() , een complete
set vormen. Dit betekent dat een willekeurige toestandsfunctie
, een complete
set vormen. Dit betekent dat een willekeurige toestandsfunctie ![]() van het systeem geëxpandeerd kan worden in termen van de
eigenfuncties van een willekeurige Hermitische operator als
van het systeem geëxpandeerd kan worden in termen van de
eigenfuncties van een willekeurige Hermitische operator als
| (13) |
Met behulp van het expansietheorema (vergelijking (12)), kunnen we de
waarschijnlijkheidsverdeling afleiden voor de resultaten van metingen
van ![]() . De verwachtingswaarde van de observabele
. De verwachtingswaarde van de observabele ![]() voor een
systeem beschreven door toestand
voor een
systeem beschreven door toestand ![]() wordt gegeven door
wordt gegeven door
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Uit de normering van de toestandsfunctie volgt dat
| (19) |
| (20) |
| (21) |
We komen dus tot de opmerkelijke conclusie dat in welke toestand
![]() het systeem ook is, als resultaat van een meting
kunnen enkel eigenwaarden zoals
het systeem ook is, als resultaat van een meting
kunnen enkel eigenwaarden zoals ![]() en
en ![]() gevonden worden en niet bijvoorbeeld een waarde tussen
gevonden worden en niet bijvoorbeeld een waarde tussen
![]() en
en ![]() . Dit is volledig anders dan we op basis van de klassieke
fysica zouden verwachten. Dit gedrag is volledig in overeenstemming met
experimentele resultaten.
. Dit is volledig anders dan we op basis van de klassieke
fysica zouden verwachten. Dit gedrag is volledig in overeenstemming met
experimentele resultaten.