



Next: IMPULSMOMENT
Up: WATERSTOFATOOM
Previous: Verstrooiing aan een gelokaliseerde
Contents
Het waterstofatoom bestaat uit een proton en een elektron.
We beschouwen de beweging van het elektron met (gereduceerde16) massa
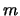 onder invloed van de Coulomb potentiaal
onder invloed van de Coulomb potentiaal
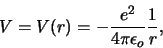 |
(478) |
met 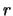 de afstand van het elektron met lading
de afstand van het elektron met lading 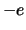 tot het proton met
lading
tot het proton met
lading 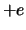 . We veronderstellen dat het proton zich in de oorsprong
bevindt. Invullen van de Coulomb potentiaal in de Schrödingervergelijking
levert
. We veronderstellen dat het proton zich in de oorsprong
bevindt. Invullen van de Coulomb potentiaal in de Schrödingervergelijking
levert
![\begin{displaymath}
\left[ -{\hbar^2 \over 2m}\Delta -{e^2 \over 4\pi\epsilon_0r} \right]
\psi (\vec r) =E\psi (\vec r) .
\end{displaymath}](img1436.png) |
(479) |
We stellen
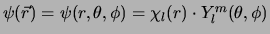 en vinden dan, met
en vinden dan, met 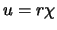 ,
voor de radiële golffunctie de differentiaalvergelijking
,
voor de radiële golffunctie de differentiaalvergelijking
![\begin{displaymath}
-{\hbar^2 \over 2m}{d^2u \over dr^2} + \left[ -{e^2 \over 4...
... r} + {\hbar^2 \over 2m}{l(l+1) \over r^2} \right] u = Eu .
\end{displaymath}](img1439.png) |
(480) |
We zien in bovenstaande vergelijking dat de Coulomb potentiaal
aantrekkend is, terwijl de 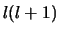 -`potentiaal' altijd afstotend is.
Dit is weergegeven in Fig. 36.
-`potentiaal' altijd afstotend is.
Dit is weergegeven in Fig. 36.
Figuur 36:
De effectieve potentiaal in de Schrödingervergelijking
voor een aantrekkende Coulomb potentiaal en 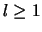 .
.
|
|
We dienen nu deze vergelijking voor 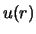 op te lossen en de
mogelijke energietoestanden te bepalen. Het waterstofatoom vormt
de hoeksteen van de quantum theorie en we zullen stap voor stap
door de afleidingen gaan.
op te lossen en de
mogelijke energietoestanden te bepalen. Het waterstofatoom vormt
de hoeksteen van de quantum theorie en we zullen stap voor stap
door de afleidingen gaan.
We beginnen met het opschonen van de notatie en definiëren
hiertoe de variabele
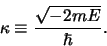 |
(481) |
Merk op dat voor gebonden toestanden geldt dat 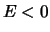 en dat
en dat
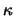 daarom reëel is. Vervolgens delen we vergelijking
(487) door
daarom reëel is. Vervolgens delen we vergelijking
(487) door 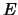 en vinden
en vinden
![\begin{displaymath}
{1 \over \kappa^2}{d^2u \over dr^2} = \left[ 1 -{me^2 \over...
...1 \over \kappa r} + {l(l+1) \over (\kappa r)^2} \right] u .
\end{displaymath}](img1444.png) |
(482) |
Vervolgens definiëren we de variabelen
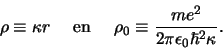 |
(483) |
De radiële vergelijking simplificeert nu tot
![\begin{displaymath}
{{\rm d}^2 u \over {\rm d}\rho^2} = \left[ 1 - {\rho_0 \over \rho}
+ {l(l+1) \over \rho^2 } \right] u.
\end{displaymath}](img1446.png) |
(484) |
We verwachten dat de oplossingen exponentieel gedempt zijn voor
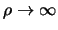 . In die limiet hebben we
. In die limiet hebben we
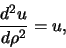 |
(485) |
met als algemene oplossing
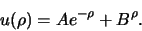 |
(486) |
De laatste term blaast weer op als
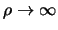 en
we kiezen daarom
en
we kiezen daarom 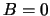 . Klaarblijkelijk geldt
. Klaarblijkelijk geldt
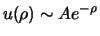 voor grote
voor grote 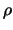 . Aan de andere kant, domineert de centrifugale term in de
limiet
. Aan de andere kant, domineert de centrifugale term in de
limiet
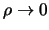 . We vinden in dat geval
. We vinden in dat geval
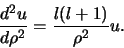 |
(487) |
De algemene oplossing hiervan is
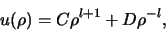 |
(488) |
zoals eenvoudig te controleren valt door dit in te vullen
in vergelijking (494). We zien dat in de limiet
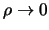 de term met
de term met 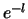 opblaast. We kiezen daarom
opblaast. We kiezen daarom
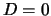 en hebben voor kleine
en hebben voor kleine 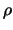 als oplossing
als oplossing
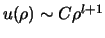 .
.
Als volgende stap proberen we nu dit asymptotische gedrag af te
scheiden, door een nieuwe functie
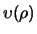 te introduceren,
te introduceren,
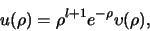 |
(489) |
in de hoop dat de differentiaalvergelijking voor
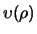 eenvoudiger wordt. De eerste afgeleide is
eenvoudiger wordt. De eerste afgeleide is
![\begin{displaymath}
{{\rm d}u \over {\rm d}\rho} = \rho^l e^{-\rho} \left[ (l+1...
...silon
+ \rho {{\rm d} \upsilon \over {\rm d} \rho} \right],
\end{displaymath}](img1459.png) |
(490) |
en de tweede afgeleide is
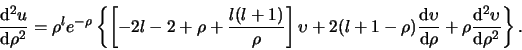 |
(491) |
We kunnen de radiële vergelijking nu herschrijven
in termen van
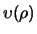 .
Dit leidt uiteindelijk tot de differentiaalvergelijking
.
Dit leidt uiteindelijk tot de differentiaalvergelijking
![\begin{displaymath}
\rho {{\rm d}^2 \upsilon \over {\rm d} \rho^2}
+ 2(l + 1 -...
...{\rm d} \rho}
+ \left[ \rho_0 -2 (l+1) \right] \upsilon = 0.
\end{displaymath}](img1461.png) |
(492) |
Bovenstaande differentiaalvergelijking kan opgelost worden
door aan te nemen dat de oplossing als een machtreeks kan worden
geschreven. We schrijven
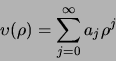 |
(493) |
en we dienen nu de coëfficiënten
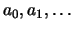 te
bepalen. Voor de eerste-orde afgeleide geldt
te
bepalen. Voor de eerste-orde afgeleide geldt
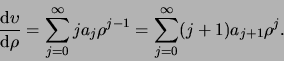 |
(494) |
Hierbij is in de tweede
sommatie de index hergedefinieerd (
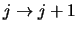 ).
Voor de tweede-orde afgeleide geldt
).
Voor de tweede-orde afgeleide geldt
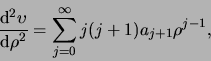 |
(495) |
Als we deze uitdrukkingen invullen in radiële vergelijking in termen van 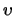 ,
vinden we
,
vinden we
![\begin{displaymath}
\sum_{j=0}^\infty j(j+1) a_{j+1}\rho^j
+ 2(l+1) \sum_{j=0}...
...t[ \rho_0 - 2(l+1) \right]
\sum_{j=0}^\infty a_j \rho^j = 0.
\end{displaymath}](img1468.png) |
(496) |
Vervolgens merken we op dat coëfficiënten behorend bij
dezelfde macht van 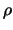 tegen elkaar weg dienen te vallen. Dit levert
tegen elkaar weg dienen te vallen. Dit levert
![\begin{displaymath}
j(j+1)a_{j+1} + 2(l+1)(j+1)a_{j+1} -2ja_j + [\rho_0 -2(l+1)]a_j =0,
\end{displaymath}](img1469.png) |
(497) |
of
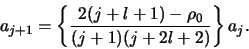 |
(498) |
Deze recursierelatie bepaalt de coëfficiënten en daarmee de
functie
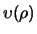 . We beginnen met
. We beginnen met 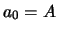 en de vergelijking
geeft ons dan
en de vergelijking
geeft ons dan 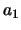 . Overigens bepalen we uiteindelijk de waarde voor
. Overigens bepalen we uiteindelijk de waarde voor 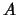 door de zaak te normeren. Vervolgens stoppen we
door de zaak te normeren. Vervolgens stoppen we 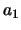 in de recursierelatie
en bepalen zo
in de recursierelatie
en bepalen zo 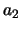 , enzovoort.
, enzovoort.
We inspecteren nu de coëfficiënten voor grote waarden
van 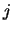 . Dat correspondeert met grote
. Dat correspondeert met grote 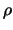 , waar de hogere
machten domineren. In dit gebied kunnen we de recursie relatie
schrijven als
, waar de hogere
machten domineren. In dit gebied kunnen we de recursie relatie
schrijven als
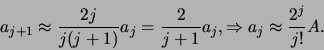 |
(499) |
Stel dat we zouden aannemen dat dit het exacte resultaat
is, dan zou gelden
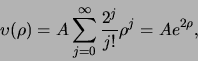 |
(500) |
en dus
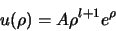 |
(501) |
en daarvan wisten we al dat dit opblaast bij grote 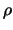 . Dit positieve
exponentiële gedrag is nou net precies wat we niet wilden hebben
in vergelijking (493). Het is trouwens niet verbazingwekkend
dat we dit hier terug vinden, omdat het nu eenmaal het asymptotische
gedrag van sommige oplossingen van de radiële vergelijking beschrijft.
Wij zijn er alleen niet geïnteresseerd in, omdat ze niet te
normeren zijn. Er is echter een uitweg uit dit dilemma: de machtreeks
dient eindig te zijn! Er moet een of andere maximale integer,
. Dit positieve
exponentiële gedrag is nou net precies wat we niet wilden hebben
in vergelijking (493). Het is trouwens niet verbazingwekkend
dat we dit hier terug vinden, omdat het nu eenmaal het asymptotische
gedrag van sommige oplossingen van de radiële vergelijking beschrijft.
Wij zijn er alleen niet geïnteresseerd in, omdat ze niet te
normeren zijn. Er is echter een uitweg uit dit dilemma: de machtreeks
dient eindig te zijn! Er moet een of andere maximale integer, 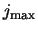 ,
bestaan, zodat
,
bestaan, zodat
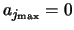 . Vanwege recursie verdwijnen alle
coëfficiënten voor hogere machten dan automatisch.
Klaarblijkelijk voldoet de recursie formule aan
. Vanwege recursie verdwijnen alle
coëfficiënten voor hogere machten dan automatisch.
Klaarblijkelijk voldoet de recursie formule aan
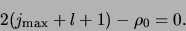 |
(502) |
We definiëren
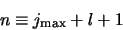 |
(503) |
als het hoofdquantumgetal en vinden
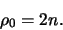 |
(504) |
We weten dat volgens vergelijkingen (488) en (490)
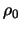 de energie
de energie 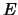 bepaalt en vinden
bepaalt en vinden
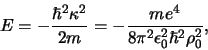 |
(505) |
en de mogelijke energiën worden gegeven door
![\begin{displaymath}
E_n = - \left[ {m \over 2\hbar^2} \left(
{e^2 \over 4 \pi...
...right] {1 \over n^2}
= {E_1 \over n^2}, n = 1,2,3,\cdots
\end{displaymath}](img1482.png) |
(506) |
Dit is de beroemde vergelijking van Bohr.
We constateren dat voor de Coulomb potentiaal, net als voor elke andere
potentiaal die tot gebonden toestanden leidt, de toegestane energieën
van een deeltje dat zich beweegt in deze potentiaal discreet
gequantiseerd is. De energieniveaus worden getoond in Fig. 37.
Figuur 37:
De laagste energieniveaus 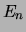 van het waterstofatoom
corresponderen met de energie eigenwaarden van de Hamiltoniaan.
van het waterstofatoom
corresponderen met de energie eigenwaarden van de Hamiltoniaan.
|
|
Als we vergelijkingen (490) en (511) combineren, vinden we
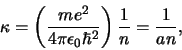 |
(507) |
waarbij
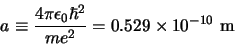 |
(508) |
de zogenaamde Bohrstraal is. Hieruit volgt dat
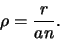 |
(509) |
De ruimtelijke golffuncties van het waterstofatoom worden gekenmerkt door
drie quantumgetallen (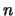 ,
, 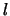 en
en 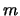 ) en worden geschreven als
) en worden geschreven als
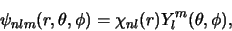 |
(510) |
waarbij volgens vergelijkingen
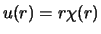 en
en
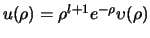 geldt dat
geldt dat
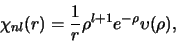 |
(511) |
met
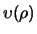 een polynoom van de orde
een polynoom van de orde
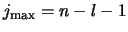 in
in 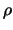 , waarvan de coëfficiënten, tot op een algemene
normeringsfactor na, bepaald worden door de recursie formule
, waarvan de coëfficiënten, tot op een algemene
normeringsfactor na, bepaald worden door de recursie formule
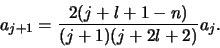 |
(512) |
Voor de grondtoestand, de toestand met laagste energie, geldt 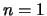 .
We vinden hiervoor
.
We vinden hiervoor
![\begin{displaymath}
E_1 = - \left[ {m \over 2\hbar^2} \left( {e^2 \over 4 \pi \epsilon_0}
\right)^2 \right] = -13,6 {\rm eV}.
\end{displaymath}](img1492.png) |
(513) |
Hieruit volgt dat de bindingsenergie, dat is de energie die het kost
om het elektron van het waterstofatoom te verwijderen (het atoom
te ioniseren), van waterstof 13,6 eV is. Volgens vergelijking (510)
is in dat geval 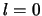 en dus ook
en dus ook 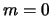 (volgens vergelijking (446))
en vinden we voor de golffunctie
(volgens vergelijking (446))
en vinden we voor de golffunctie
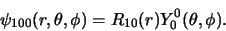 |
(514) |
De recursie formule breekt af na de eerste term. Daarom is
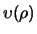 een constante (
een constante (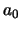 ) en
) en
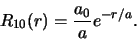 |
(515) |
Als we dit normeren vinden we
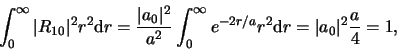 |
(516) |
waaruit volgt dat
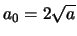 . Verder geldt
. Verder geldt
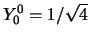 en dus
en dus
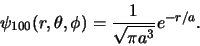 |
(517) |
Voor 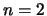 is de energie gelijk aan
is de energie gelijk aan
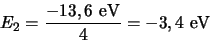 |
(518) |
en dit is de eerste aangeslagen toestand van het waterstofatoom.
Preciezer gezegd, de eerste aangeslagen toestanden, want we kunnen
nu zowel 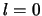 (waarvoor geldt
(waarvoor geldt 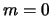 ) als
) als 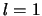 (met
(met 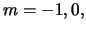 of +1)
hebben. Voor
of +1)
hebben. Voor 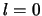 geldt dan
geldt dan
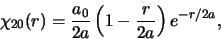 |
(519) |
terwijl voor 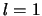 geldt dat
geldt dat
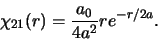 |
(520) |
In beide gevallen dienen we de constante 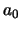 uit de normering te
bepalen.
Fig. 38 toont enkele radiële
waarschijnlijkheidsdichtheden voor het waterstofatoom.
uit de normering te
bepalen.
Fig. 38 toont enkele radiële
waarschijnlijkheidsdichtheden voor het waterstofatoom.
Figuur 38:
De radiële waarschijnlijkheidsdichtheid voor het
elektron in het waterstofatoom voor diverse quantumgetallen 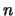 en
en 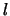 .
.
|
|
De laagste-orde radiële golffuncties van een één-elektron
atoom kunnen expliciet geschreven worden als
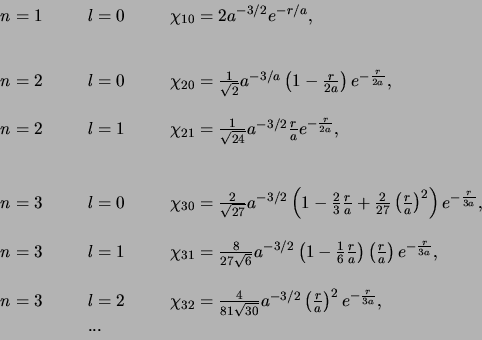 |
(521) |
Voor willekeurige waarden van 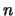 zijn de mogelijke waarden van
zijn de mogelijke waarden van 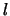 gelijk aan
gelijk aan
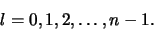 |
(522) |
Voor elke 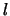 zijn er
zijn er 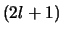 mogelijke waarden van
mogelijke waarden van 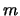 , zodat
de totale ontaardheid van energieniveau
, zodat
de totale ontaardheid van energieniveau 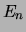 gelijk is aan
gelijk is aan
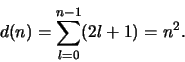 |
(523) |
Overigens is de polynoom
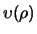 een bekende wiskundige
functie (afgezien van de normering) en kan geschreven worden als
een bekende wiskundige
functie (afgezien van de normering) en kan geschreven worden als
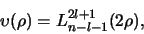 |
(524) |
met
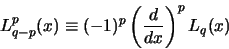 |
(525) |
de geassocieerde Laguerre polynoom en
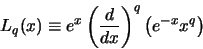 |
(526) |
de 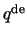 Laguerre polynoom. Hiermee kunnen we de
genormeerde golffuncties voor het waterstofatoom schrijven als
Laguerre polynoom. Hiermee kunnen we de
genormeerde golffuncties voor het waterstofatoom schrijven als
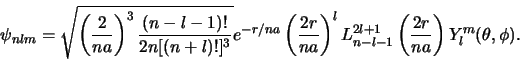 |
(527) |
Met bovenstaande uitdrukking hebben we een oplossing gevonden
voor een van de weinige realistische systemen die we zonder de
hulp van een computer kunnen beschrijven. Overigens kunnen we
ook nog bewijzen dat de oplossingen onderling orthogonaal zijn,
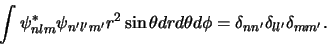 |
(528) |
Figuur 39:
Spectra voor het normale Lorentz triplet in zink en het anomaal
Zeeman effect in kalium en in zink.
|
|
Tenslotte tonen we in Fig. 39 de experimentele observatie
van de opsplitsing van de spectraallijnen van diverse elementen
in een zwak magnetisch veld. Het verband tussen de structuur van de
multipletten en het periodiek systeem leidde tot de uiteindelijke
ontdekking van spin. Wolfgang Pauli kende deze eigenschap toe aan het
elektron, waarbij hij twee waarden van spin toeliet. Dit betekende
effectief het invoeren van een vierde quantumgetal in de beschrijving
van elk atomair elektron.




Next: IMPULSMOMENT
Up: WATERSTOFATOOM
Previous: Verstrooiing aan een gelokaliseerde
Contents
Jo van den Brand
2004-09-25
![\begin{displaymath}
\left[ -{\hbar^2 \over 2m}\Delta -{e^2 \over 4\pi\epsilon_0r} \right]
\psi (\vec r) =E\psi (\vec r) .
\end{displaymath}](img1436.png)
![\includegraphics[width=12cm]{Figures/Fig25.eps}](img1440.png)
![]() op te lossen en de
mogelijke energietoestanden te bepalen. Het waterstofatoom vormt
de hoeksteen van de quantum theorie en we zullen stap voor stap
door de afleidingen gaan.
op te lossen en de
mogelijke energietoestanden te bepalen. Het waterstofatoom vormt
de hoeksteen van de quantum theorie en we zullen stap voor stap
door de afleidingen gaan.
![\begin{displaymath}
{{\rm d}^2 u \over {\rm d}\rho^2} = \left[ 1 - {\rho_0 \over \rho}
+ {l(l+1) \over \rho^2 } \right] u.
\end{displaymath}](img1446.png)
![]() te introduceren,
te introduceren,
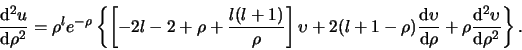
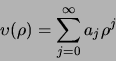
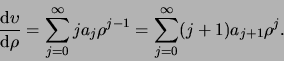
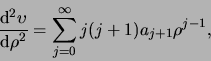
![\begin{displaymath}
\sum_{j=0}^\infty j(j+1) a_{j+1}\rho^j
+ 2(l+1) \sum_{j=0}...
...t[ \rho_0 - 2(l+1) \right]
\sum_{j=0}^\infty a_j \rho^j = 0.
\end{displaymath}](img1468.png)
![]() . Dat correspondeert met grote
. Dat correspondeert met grote ![]() , waar de hogere
machten domineren. In dit gebied kunnen we de recursie relatie
schrijven als
, waar de hogere
machten domineren. In dit gebied kunnen we de recursie relatie
schrijven als
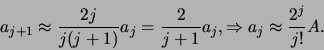
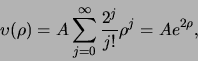
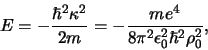
![\begin{displaymath}
E_n = - \left[ {m \over 2\hbar^2} \left(
{e^2 \over 4 \pi...
...right] {1 \over n^2}
= {E_1 \over n^2}, n = 1,2,3,\cdots
\end{displaymath}](img1482.png)
![\includegraphics[width=14cm]{Figures/Fig27.eps}](img1483.png)
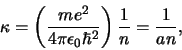
![]() .
We vinden hiervoor
.
We vinden hiervoor
![\begin{displaymath}
E_1 = - \left[ {m \over 2\hbar^2} \left( {e^2 \over 4 \pi \epsilon_0}
\right)^2 \right] = -13,6 {\rm eV}.
\end{displaymath}](img1492.png)
![]() is de energie gelijk aan
is de energie gelijk aan
![\includegraphics[width=12cm]{Figures/Fig26.eps}](img1506.png)
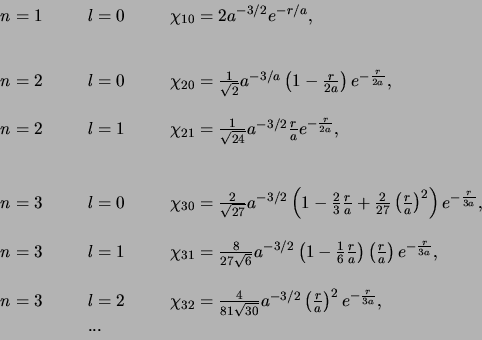
![]() zijn de mogelijke waarden van
zijn de mogelijke waarden van ![]() gelijk aan
gelijk aan
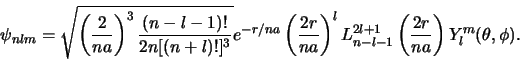
![\includegraphics[width=10cm]{Figures/Fig28.eps}](img1516.png)