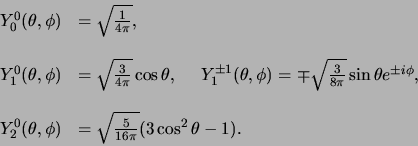Next: Radiële oplossingen
Up: Schrödingervergelijking in drie dimensies
Previous: Scheiden van variabelen
Contents
De eerste vergelijking in uitdrukking (437)
heeft als oplossing
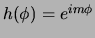 .
We dienen nu de eis te stellen dat de oplossing eenduidig
is, hetgeen van speciaal belang is voor de hoeken
.
We dienen nu de eis te stellen dat de oplossing eenduidig
is, hetgeen van speciaal belang is voor de hoeken
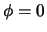 en
en 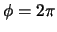 . We krijgen hiermee
. We krijgen hiermee
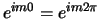 en dus
en dus
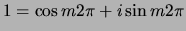 .
Aan deze eis kan enkel voldaan worden in geval
.
Aan deze eis kan enkel voldaan worden in geval
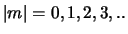 .
Het is duidelijk dat er quantisatie van de richting optreedt.
In de klassieke fysica zouden we de hoekafhankelijkheid als
sin- en cos-functies opschrijven, omdat de hoekenfuncties reëel
dienen te zijn. In de quantummechanica bestaat een dergelijke
beperking niet.
We zien dat de oplossing voor de
.
Het is duidelijk dat er quantisatie van de richting optreedt.
In de klassieke fysica zouden we de hoekafhankelijkheid als
sin- en cos-functies opschrijven, omdat de hoekenfuncties reëel
dienen te zijn. In de quantummechanica bestaat een dergelijke
beperking niet.
We zien dat de oplossing voor de 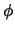 afhankelijkheid de
Schrödingervergelijking gegeven wordt door
afhankelijkheid de
Schrödingervergelijking gegeven wordt door 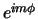 . We
noemen
. We
noemen 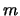 het magnetisch quantumgetal.
het magnetisch quantumgetal.
De tweede vergelijking kan herschreven worden tot
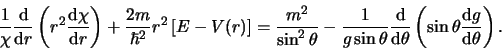 |
(432) |
In bovenstaande vergelijking zijn we er in geslaagd de variabelen
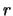 en
en 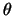 te scheiden. We voeren dan ook een scheidingsconstante
in en kiezen hiervoor
te scheiden. We voeren dan ook een scheidingsconstante
in en kiezen hiervoor 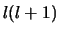 . We vinden dan de
twee differentiaalvergelijkingen
. We vinden dan de
twee differentiaalvergelijkingen
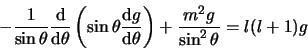 |
(433) |
en
![\begin{displaymath}
{1 \over r^2} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d...
...2} \left[ E - V(r) \right] \chi =
l(l+1) {\chi \over r^2} .
\end{displaymath}](img1329.png) |
(434) |
Als we de differentiaalvergelijking voor de 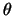 afhankelijkheid
oplossen15,
dan vinden we dat eindige oplossingen slechts
verkregen kunnen worden indien
afhankelijkheid
oplossen15,
dan vinden we dat eindige oplossingen slechts
verkregen kunnen worden indien
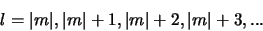 |
(439) |
Deze oplossingen kunnen geschreven worden als
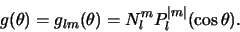 |
(440) |
We herkennen in de functies
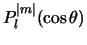 de
Legendre functies die polynomen zijn in
de
Legendre functies die polynomen zijn in  en waarvan de
vorm afhangt van de waarde van het quantumgetal
en waarvan de
vorm afhangt van de waarde van het quantumgetal 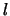 en de absolute
waarde van het quantumgetal
en de absolute
waarde van het quantumgetal 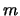 .
De geassocieerde
Legendre functie worden gedefinieerd door de vergelijking
.
De geassocieerde
Legendre functie worden gedefinieerd door de vergelijking
![\begin{displaymath}
P_l^{\vert m \vert} (\mu ) = {1 \over 2^ll!} (1-\mu^2 )^{\v...
... \vert} \over {\rm d}\mu^{l+ \vert m \vert}}
[(\mu^2 -1)^l]
\end{displaymath}](img1339.png) |
(441) |
en de normalisatie constanten door
![\begin{displaymath}
N_l^m = (-1)^{(m+\vert m \vert )/2} \left[ {2l+1 \over 4\pi...
...l-\vert m \vert )! \over (l+\vert m \vert )!} \right]^{1/2} .
\end{displaymath}](img1340.png) |
(442) |
De complete hoekafhankelijkheid wordt in het geval van een
centrale potentiaal, hierbij doet de exacte vorm van deze potentiaal
niet terzake, gegeven door de zogenaamde sferisch harmonische
functies,
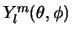 . De functies
. De functies
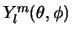 kunnen expliciet geschreven worden als
kunnen expliciet geschreven worden als
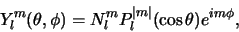 |
(443) |
De laagste-orde sferisch harmonische functies worden gegeven door
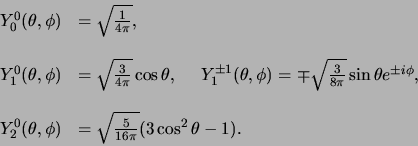 |
(444) |
De sferisch harmonische functies
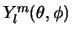 zijn in de
functieruimte van de kwadratisch integreerbare functies gedefinieerd
op de eenheidsbol. De functies voldoen aan orthogonaliteit. Er geldt
zijn in de
functieruimte van de kwadratisch integreerbare functies gedefinieerd
op de eenheidsbol. De functies voldoen aan orthogonaliteit. Er geldt
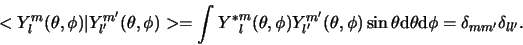 |
(445) |
We kunnen nu de algemene oplossingen van de Schrödingervergelijking
voor een centrale potentiaal dus schrijven als
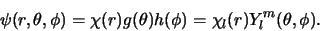 |
(446) |
In de volgende paragraaf beschouwen we het radiële deel nader.




Next: Radiële oplossingen
Up: Schrödingervergelijking in drie dimensies
Previous: Scheiden van variabelen
Contents
Jo van den Brand
2004-09-25
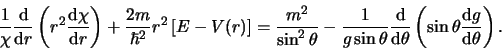
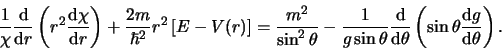
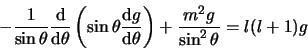
![\begin{displaymath}
P_l^{\vert m \vert} (\mu ) = {1 \over 2^ll!} (1-\mu^2 )^{\v...
... \vert} \over {\rm d}\mu^{l+ \vert m \vert}}
[(\mu^2 -1)^l]
\end{displaymath}](img1339.png)
![\begin{displaymath}
N_l^m = (-1)^{(m+\vert m \vert )/2} \left[ {2l+1 \over 4\pi...
...l-\vert m \vert )! \over (l+\vert m \vert )!} \right]^{1/2} .
\end{displaymath}](img1340.png)
![]() . De functies
. De functies
![]() kunnen expliciet geschreven worden als
kunnen expliciet geschreven worden als