Next: Verstrooiing aan een gelokaliseerde
Up: Centrale vierkante sferische potentiaal
Previous: Oplossing oneindige potentiaal put
Contents
De algemene oplossing van de radiële vergelijking
voor de oneindige potentiaal put wordt gegeven door
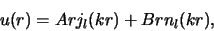 |
(459) |
met 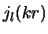 de sferische Bessel functie van de
orde
de sferische Bessel functie van de
orde 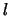 en
en 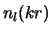 de sferische Neumann functie
van de orde
de sferische Neumann functie
van de orde 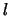 .
Deze functies zijn gedefinieerd als
.
Deze functies zijn gedefinieerd als
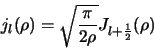 |
(460) |
en
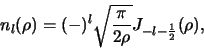 |
(461) |
met 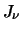 de normale Besselfunctie van de orde
de normale Besselfunctie van de orde 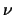 .
Merk op dat
.
Merk op dat 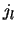 en
en 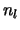 reëele functies zijn.
Fig. 34 toont enkele van de reguliere Besselfuncties.
reëele functies zijn.
Fig. 34 toont enkele van de reguliere Besselfuncties.
Figuur 34:
Reguliere Besselfuncties die het radiële deel van
de golffunctie beschrijven van een deeltje dat zich in een
potentiaal put beweegt.
|
|
De laagste-orde sferische Bessel en Neumann functies zijn
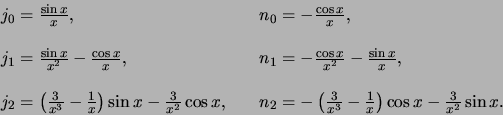 |
(462) |
Merk op dat voor kleine  geldt dat
geldt dat
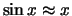 en
en
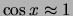 . We zien dan dat enkel de Bessel functies
eindig blijven bij de oorsprong, terwijl de Neumann functies
naar oneindig gaan. Daarom dient te gelden dat
. We zien dan dat enkel de Bessel functies
eindig blijven bij de oorsprong, terwijl de Neumann functies
naar oneindig gaan. Daarom dient te gelden dat 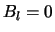 en
we vinden
en
we vinden
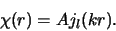 |
(463) |
Verder hebben we nog de randvoorwaarde 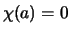 en
dienen we
en
dienen we 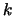 zo te kiezen dat
zo te kiezen dat 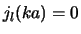 . Nu is
het zo dat iedere Bessel functie oneindig veel nulpunten
heeft. We noemen
. Nu is
het zo dat iedere Bessel functie oneindig veel nulpunten
heeft. We noemen 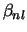 het
het 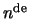 -nulpunt
van de
-nulpunt
van de 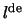 sferische Bessel functie. Er dient
dan te gelden dat
sferische Bessel functie. Er dient
dan te gelden dat
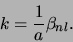 |
(464) |
De mogelijke energietoestanden zijn dan gegeven door
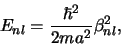 |
(465) |
en de golffuncties door
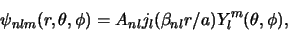 |
(466) |
waarbij we de constante 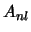 weer uit de normeringsconditie
kunnen bepalen. We zien dat elk energieniveau
weer uit de normeringsconditie
kunnen bepalen. We zien dat elk energieniveau 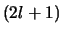 -keer
ontaard is, omdat er
-keer
ontaard is, omdat er 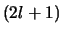 verschillende waarden voor
verschillende waarden voor 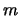 zijn bij elke waarde van
zijn bij elke waarde van 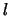 .
.




Next: Verstrooiing aan een gelokaliseerde
Up: Centrale vierkante sferische potentiaal
Previous: Oplossing oneindige potentiaal put
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=12cm]{Figures/Fig24.eps}](img1383.png)