



Next: Algemene oplossing oneindige potentiaal
Up: Centrale vierkante sferische potentiaal
Previous: Centrale vierkante sferische potentiaal
Contents
In het geval dat 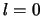 gaat vergelijking (460) over in
gaat vergelijking (460) over in
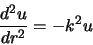 |
(455) |
en vinden we als oplossing
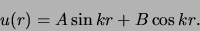 |
(456) |
Voor de radiële golffunctie geldt dan
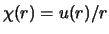 .
Omdat
.
Omdat
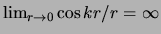 , dienen
we
, dienen
we 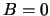 te kiezen. De randvoorwaarde vereist dan
te kiezen. De randvoorwaarde vereist dan 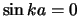 en dus
en dus 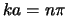 , voor
, voor
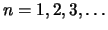 . De toegestane
energieniveaus zijn dus
. De toegestane
energieniveaus zijn dus
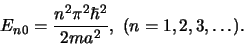 |
(457) |
Dit is hetzelfde resultaat als we eerder in hoofdstuk 4.3
en 5.3 gevonden hebben.
Als we 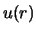 normeren vinden we
normeren vinden we
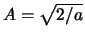 en als we het
hoekgedeelte meenemen (dat is overigens constant, omdat
en als we het
hoekgedeelte meenemen (dat is overigens constant, omdat
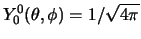 ), vinden we
), vinden we
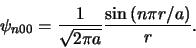 |
(458) |
We voorzien de stationaire toestanden van de labels 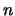 ,
, 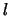 en
en 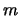 :
:
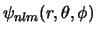 . De toestanden hangen
van deze drie quantum getallen af. De energie hangt
enkel af van
. De toestanden hangen
van deze drie quantum getallen af. De energie hangt
enkel af van 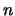 en
en 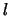 :
: 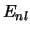 .
.




Next: Algemene oplossing oneindige potentiaal
Up: Centrale vierkante sferische potentiaal
Previous: Centrale vierkante sferische potentiaal
Contents
Jo van den Brand
2004-09-25
![]() normeren vinden we
normeren vinden we
![]() en als we het
hoekgedeelte meenemen (dat is overigens constant, omdat
en als we het
hoekgedeelte meenemen (dat is overigens constant, omdat
![]() ), vinden we
), vinden we