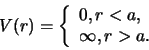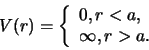Centrale vierkante sferische potentiaal put

We gaan een deeltje nu opsluiten in een drie-dimensionale put met oneindig hoge potentiaal. We hebben dit reeds eerder bestudeerd voor het één-dimensionale geval in hoofdstuk 4.3 en 5.3. Hier bespreken we een opsluiting in drie dimensies. Voor de potentiaal geldt

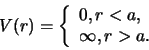$$V(r) = \left\{ \begin{array}{l} 0, r<a, \\ \infty , r>a. \end{array} \right.$$ (452)

De golffunctie is dan nul buiten de put, terwijl de golffunctie binnen de put gegeven wordt door de radiële vergelijking

$${d^2u \over dr^2} = \left[ {l(l+1) \over r^2} - k^2 \right] u ,$$ (453)

waarbij we voor 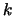$k$ de definitie

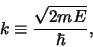$$k \equiv {\sqrt{2mE} \over \hbar},$$ (454)

gebruiken.