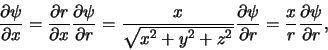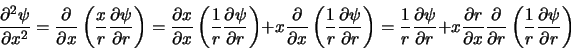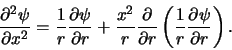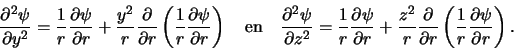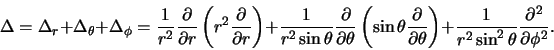Next: Schrödingervergelijking in drie dimensies
Up: WATERSTOFATOOM
Previous: WATERSTOFATOOM
Contents
Tot nu toe hebben de discussie veelal beperkt tot één dimensie. Hier beschouwen
we systemen in drie dimensies en om een en ander te verduidelijken gebruiken
we vetgedrukte letters om operatoren aan te duiden en pijltjes om het
vectorgedrag aan te geven.
Verder hebben we grootheden enkel
beschreven in een cartesisch coördinatensysteem. Echter, als
het natuurkundig verschijnsel dat we willen beschrijven sferische symmetrie
heeft, dan is het voordelig om een sferisch coördinatensysteem te gebruiken.
Beide systemen worden getoond in figuur 33.
Figuur 33:
De sferische coördinaten  ,
, 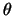 en
en 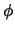 van een punt
van een punt 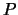 en de bijbehorende cartesische coördinaten
en de bijbehorende cartesische coördinaten
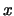 ,
, 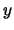 en
en 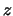 .
.
|
|
De coördinaten in beide stelsels staan met elkaar in verband
volgens
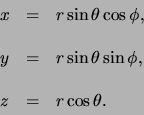 |
(408) |
Verder geldt de relatie
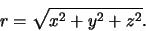 |
(409) |
In hoofdstuk 7.2.4 zijn we voor het eerst de tijdonafhankelijke
Schrödingervergelijking in drie dimensies tegengekomen,
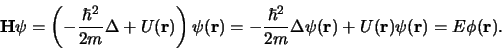 |
(410) |
De operator aan de linkerkant noemt men de Hamilton operator
of Hamiltoniaan. De verschillende energietoestanden van het waterstofatoom
zijn stationaire toestanden en dat zijn eigenfuncties van deze
Hamiltoniaan,
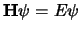 .
De eerste term correspondeert met de operator voor de kinetische energie
van een deeltje en is analoog aan de klassieke uitdrukking
.
De eerste term correspondeert met de operator voor de kinetische energie
van een deeltje en is analoog aan de klassieke uitdrukking
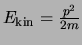 .
We schrijven,
.
We schrijven,
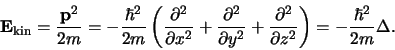 |
(411) |
De operator 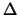 is de zogenaamde Laplace operator met als definitie
is de zogenaamde Laplace operator met als definitie
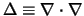 . De tweede term correspondeert
met de operator voor potentiële energie,
. De tweede term correspondeert
met de operator voor potentiële energie,
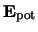 .
.
In cartesische coördinaten heeft de impulsoperator in drie dimensies de vorm
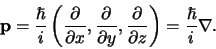 |
(412) |
De operator die correspondeert met de volledige impulsvector van een
deeltje is dus de gradiënt operator, vermenigvuldigd met
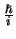 .
.
Teneinde de Laplace operator in sferische coördinaten te vinden,
dienen we afgeleiden te nemen. Een
elegante manier om deze uitdrukkingen af te leiden, is door gebruik
te maken van matrixnotatie. Er geldt
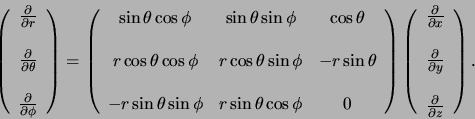 |
(413) |
We kunnen deze matrix inverteren en verkrijgen op deze wijze uitdrukkingen
voor de operatoren
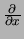 ,
,
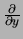 en
en
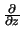 . Er geldt
. Er geldt
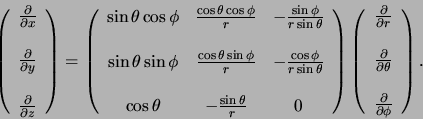 |
(414) |
We kunnen de juistheid van bovenstaande uitdrukking controleren
door de twee matrices te vermenigvuldigen, waarbij het resultaat
de eenheidsmatrix dient te zijn.
De Laplace operator is een ingrediënt van de Schrödingervergelijking
en wordt in een cartesisch coördinatensysteem geschreven als
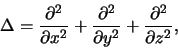 |
(415) |
terwijl in een sferisch coördinatensysteem geldt dat
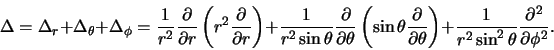 |
(416) |
We kunnen de eerste term, 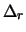 van de Laplace operator in sferische
coördinaten vinden door aan te nemen dat de golffunctie
enkel een functie is van
van de Laplace operator in sferische
coördinaten vinden door aan te nemen dat de golffunctie
enkel een functie is van 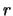 en dus geldt
en dus geldt
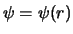 .
Met behulp van de kettingregel vinden we dan
.
Met behulp van de kettingregel vinden we dan
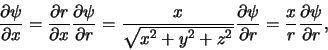 |
(417) |
terwijl voor de tweede-orde afgeleide geldt
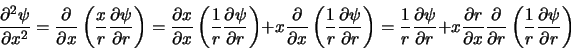 |
(418) |
en dus
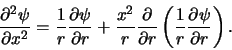 |
(419) |
Op dezelfde manier kunnen we de afgeleiden naar 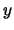 en
en 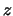 uitrekenen
en vinden
uitrekenen
en vinden
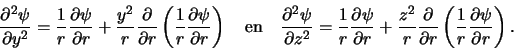 |
(420) |
Als we de laatste drie vergelijkingen optellen, dan vinden we
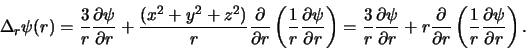 |
(421) |
We kunnen bovenstaande vergelijking omschrijven tot
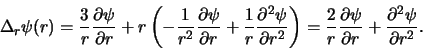 |
(422) |
Hiermee hebben we de eerste term, 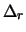 van de Laplace operator in sferische
coördinaten gevonden. In de afleiding hebben we aangenomen dat
de golffunctie enkel een functie is van
van de Laplace operator in sferische
coördinaten gevonden. In de afleiding hebben we aangenomen dat
de golffunctie enkel een functie is van 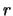 , dus geldt
, dus geldt
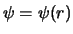 .
Merk op dat
.
Merk op dat
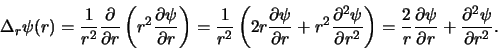 |
(423) |
De tweede en derde term, respectievelijk 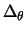 en
en 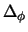 ,
in de uitdrukking voor de Laplace operator
in sferische coördinaten kunnen we vinden door eerst
,
in de uitdrukking voor de Laplace operator
in sferische coördinaten kunnen we vinden door eerst
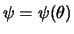 en vervolgens
en vervolgens
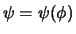 aan te nemen. Het resultaat is
aan te nemen. Het resultaat is
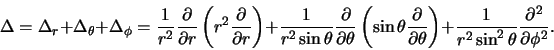 |
(424) |




Next: Schrödingervergelijking in drie dimensies
Up: WATERSTOFATOOM
Previous: WATERSTOFATOOM
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=12cm]{Figures/Fig20.eps}](img1282.png)
![\includegraphics[width=12cm]{Figures/Fig20.eps}](img1282.png)
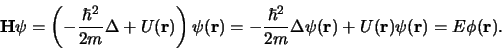
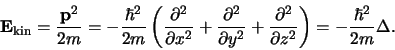
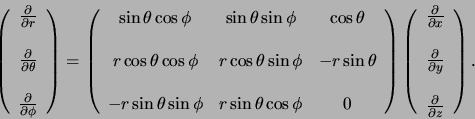
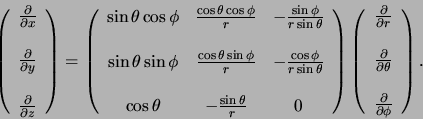
![]() van de Laplace operator in sferische
coördinaten vinden door aan te nemen dat de golffunctie
enkel een functie is van
van de Laplace operator in sferische
coördinaten vinden door aan te nemen dat de golffunctie
enkel een functie is van ![]() en dus geldt
en dus geldt
![]() .
Met behulp van de kettingregel vinden we dan
.
Met behulp van de kettingregel vinden we dan