



Next: Orthogonale matrices
Up: Matrixrekening
Previous: Geadjugeerde en inverse matrices
Contents
Als
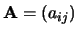 een
een 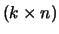 -matrix is en
-matrix is en
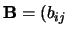 een
een 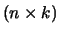 -matrix, terwijl
-matrix, terwijl
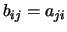 voor elke
voor elke 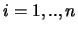 en elke
en elke 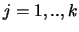 , dan heten
, dan heten  en
en 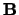 elkaars getransponeerde,
elkaars getransponeerde,
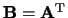 en
en
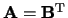 .
.
Voorbeeld: De getransponeerde van
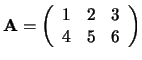 is
is
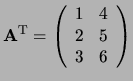 .
.
- De getransponeerde van een vierkante matrix wordt dus verkregen door
die matrix te `spiegelen ten opzichte van de hoofddiagonaal'.
- De getransponeerde van een kolomvector is een rijvector en omgekeerd.
Stellingen:
-
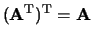 .
.
-
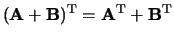 .
.
-
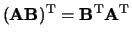 .
.
- Als
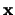 een kolomvector is dan is
een kolomvector is dan is
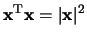 .
.
Definities:  heet een symmetrische matrix als
heet een symmetrische matrix als
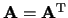 .
.
 heet een alternerende (anti-symmetrische
of scheefsymmetrische) matrix als
heet een alternerende (anti-symmetrische
of scheefsymmetrische) matrix als
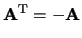 .
.
Voorbeeld: De matrix
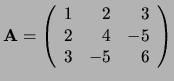 is symmetrisch, terwijl de matrix
is symmetrisch, terwijl de matrix
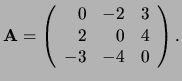 anti-symmetrisch is.
anti-symmetrisch is.
Jo van den Brand
2004-09-25
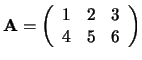 is
is
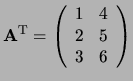 .
.
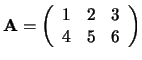 is
is
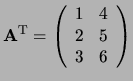 .
.
![]() heet een symmetrische matrix als
heet een symmetrische matrix als
![]() .
.
![]() heet een alternerende (anti-symmetrische
of scheefsymmetrische) matrix als
heet een alternerende (anti-symmetrische
of scheefsymmetrische) matrix als
![]() .
.
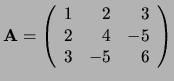 is symmetrisch, terwijl de matrix
is symmetrisch, terwijl de matrix
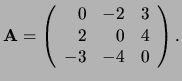 anti-symmetrisch is.
anti-symmetrisch is.