Orthogonale matrices

Definitie: De matrix ${\bf A}$ heet orthogonaal als ${\bf AA}^{\rm T} = {\bf A}^{\rm T}{\bf A} = {\bf I}$, dus als ${\bf A}^{\rm T} = {\bf A}^{-1}$.

Stelling 1: Een orthogonale matrix is een matrix waarvan de rijvectoren zowel als de kolomvectoren een orthonormaal stelsel vormen (dit wil zeggen dat elke twee onderling verschillende rijvectoren, respectievelijk kolomvectoren, onderling orthogonaal zijn, terwijl al die vectoren de norm 1 hebben.

Stelling 2: Als ${\bf A}$ orthogonaal is, dan geldt voor elke ${\bf x}$ (van de juiste dimensie) dat $\vert {\bf Ax} \vert = \vert {\bf x} \vert$. We concluderen dat de norm van een vector is invariant voor een transformatie waarvan de transformatiematrix orthogonaal is. Het omgekeerde van deze stelling geldt ook: als voor een lineaire afbeelding de norm invariant is, dan is de transformatiematrix orthogonaal.

Bewijs: $\vert {\bf Ax} \vert^2 = ({\bf Ax})^{\rm T} ({\bf Ax}) = ({\bf x}^{\rm T} {\b... ...f x}^{\rm T} {\bf I} {\bf x} = {\bf x}^{\rm T}{\bf x} = \vert {\bf x} \vert^2$.

Voorbeeld: De lineaire transformatie 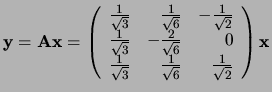${\bf y} = {\bf Ax} = \left( \begin{array}{rrr} {1 \over \sqrt{3}} & {1 \over... ...3}} & {1 \over \sqrt{6}} & {1 \over \sqrt{2}} \\ \end{array} \right) {\bf x}$ is orthogonaal. Het beeld van ${\bf x} = (a,b,c)$ is ${\bf y} = \left( {a \over \sqrt{3}} + {b \over \sqrt{6}} - {c \over \sqrt{2}}... ...sqrt{6}}, {a \over \sqrt{3}} + {b \over \sqrt{6}} + {c \over \sqrt{2}} \right)$ en beide vectoren hebben lengte $\sqrt{a^2+b^2+c^2}$.