Definitie: Als
Definitie: Als
![]() , dan heet
, dan heet ![]() een
rechterinverse van
een
rechterinverse van ![]() en
en ![]() een linkerinverse
van
een linkerinverse
van ![]() .
.
Voorbeeld: Omdat
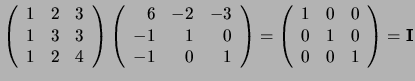 , is iedere matrix in het product de inverse van de ander.
, is iedere matrix in het product de inverse van de ander.
Stelling 1: Als ![]() een
een ![]() -matrix is,
-matrix is,
![]() en
en
![]() ,
dan
,
dan
![]() .
Bewijs:
.
Bewijs:
![]() .
.
Stelling 2: Als
![]() en
en
![]() , dan is
, dan is
![]() vierkant.
Bewijs: Als
vierkant.
Bewijs: Als
![]() , dan
, dan
![]() ,
,
![]() ,
en
,
en
![]() .
De som van de diagonaalelementen van respectievelijk
.
De som van de diagonaalelementen van respectievelijk ![]() en
en ![]() is dan
is dan
![]() en
en
![]() , dus
, dus ![]() .
.
Definitie: Als
![]() dan heten
dan heten ![]() en
en ![]() elkaars inverse matrix:
elkaars inverse matrix:
![]() en
en
![]() .
Een matrix die een inverse heeft heet regulier, terwijl een matrix
die geen inverse heeft singulier heet. Iedere reguliere matrix is
vierkant. Als
.
Een matrix die een inverse heeft heet regulier, terwijl een matrix
die geen inverse heeft singulier heet. Iedere reguliere matrix is
vierkant. Als ![]() regulier is dan heeft
regulier is dan heeft
![]() juist
één oplossing, namelijk
juist
één oplossing, namelijk
![]() .
.
Door gebruik te maken van de definities van de determinant, kan men
laten zien dat
| (241) |
Een matrix is dan en slechts dan regulier als zijn determinant ongelijk
is aan nul. Een vierkante matrix is dan en slechts dan singulier als zijn
determinant gelijk is aan nul.
Voorbeeld: Als
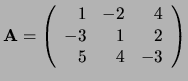 , dan
, dan
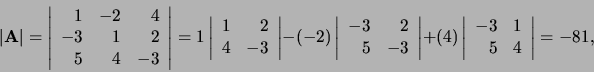 |
(242) |
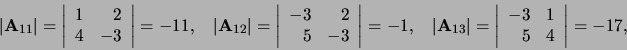 |
(243) |
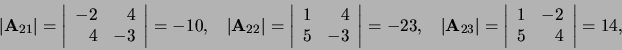 |
(244) |
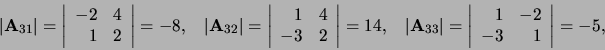 |
(245) |
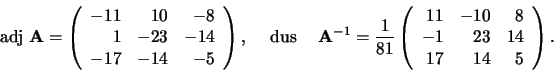 |
(246) |