



Next: Geadjugeerde en inverse matrices
Up: Matrixrekening
Previous: Product van matrices
Contents
Onder de hoofddiagonaal van een vierkante matrix
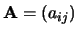 van de
van de 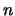 -de orde verstaan we de getallenrij
-de orde verstaan we de getallenrij
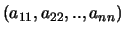 .
Een diagonale matrix is een vierkante matrix
.
Een diagonale matrix is een vierkante matrix
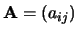 ,
waarvoor geldt, dat
,
waarvoor geldt, dat 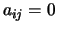 als
als 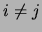 , terwijl er minstens één
, terwijl er minstens één
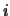 is waarvoor
is waarvoor 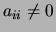 . Alleen in de hoofddiagonaal staan dus
elementen die ongelijk nul zijn.
. Alleen in de hoofddiagonaal staan dus
elementen die ongelijk nul zijn.
Als 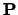 een diagonale matrix is waarvan alle diagonaalelementen gelijk
is aan
een diagonale matrix is waarvan alle diagonaalelementen gelijk
is aan 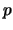 zijn en
zijn en 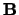 een zodanige matrix is, dat
een zodanige matrix is, dat 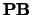 ,
respectievelijk
,
respectievelijk 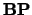 bestaat, dan is volgens de definitie van
matrixvermenigvuldiging en vermenigvuldigen met een scalar
bestaat, dan is volgens de definitie van
matrixvermenigvuldiging en vermenigvuldigen met een scalar
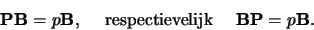 |
(240) |
Een diagonale matrix, waarvan alle diagonaaltermen onderling gelijk zijn
heet daarom een scalaire matrix. Een scalaire matrix, waarvan
alle diagonaaltermen gelijk zijn aan 1 wordt aangeduid met de letter 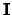 .
Zo een eenheidsmatrix I is neutraal element ten opzichte
van matrixvermenigvuldiging.
.
Zo een eenheidsmatrix I is neutraal element ten opzichte
van matrixvermenigvuldiging.
Jo van den Brand
2004-09-25
![]() een diagonale matrix is waarvan alle diagonaalelementen gelijk
is aan
een diagonale matrix is waarvan alle diagonaalelementen gelijk
is aan ![]() zijn en
zijn en ![]() een zodanige matrix is, dat
een zodanige matrix is, dat ![]() ,
respectievelijk
,
respectievelijk ![]() bestaat, dan is volgens de definitie van
matrixvermenigvuldiging en vermenigvuldigen met een scalar
bestaat, dan is volgens de definitie van
matrixvermenigvuldiging en vermenigvuldigen met een scalar