



Next: Lineaire afhankelijkheid; ontbinden van
Up: Vectorrekening over de reële
Previous: Product van een scalar
Contents
Elke twee vectoren  en
en 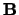 hebben een som,
hebben een som,
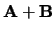 . Als het beginpunt van de pijl die B representeert
samenvalt met het eindpunt van de pijl die
. Als het beginpunt van de pijl die B representeert
samenvalt met het eindpunt van de pijl die  voorstelt, dan wordt
voorstelt, dan wordt
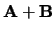 gerepresenteerd door de pijl vanaf het beginpunt van
de
gerepresenteerd door de pijl vanaf het beginpunt van
de  -pijl naar het eindpunt van de
-pijl naar het eindpunt van de 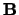 -pijl. Dit wordt
weergegeven in Fig. 1.
-pijl. Dit wordt
weergegeven in Fig. 1.
Voor optellen van vectoren gelden de axioma's
-
![$\forall_{{\bf A},{\bf B}} [ {\bf A} + {\bf B} = {\bf B} + {\bf A} ]$](img89.png) commutatieve eigenschap
commutatieve eigenschap
-
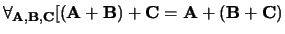 associatieve eigenschap
associatieve eigenschap
-
![$\exists_{\bf0} \forall_{\bf A} [ {\bf A} + {\bf0} = {\bf A} ]$](img91.png)
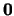 heet het neutrale element
heet het neutrale element
-
![$\forall_{\bf A} \exists_{- \bf A} [ {\bf A} + (-{\bf A}) = {\bf0} ]$](img93.png) inversiteits eigenschap
inversiteits eigenschap
Voor vermenigvuldigen van vectoren met scalaren gelden de axioma's
-
![$\forall_{p,q,{\bf A}} [ (p+q){\bf A} = p{\bf A} + q{\bf A} ]$](img94.png) eerste distributieve eigenschap
eerste distributieve eigenschap
-
![$\forall_{p,{\bf A},{\bf B}} [ p({\bf A} + {\bf B}) = p{\bf A} + p{\bf B} ]$](img95.png) tweede distributieve eigenschap
tweede distributieve eigenschap
-
![$\forall_{p,q,{\bf A}} [ p(q{\bf A}) = (pq){\bf A} ]$](img96.png) associatieve eigenschap
associatieve eigenschap
-
![$\forall_{\bf A} [ 1{\bf A} = {\bf A} ]$](img97.png) neutraliteitseigenschap van het getal 1.
neutraliteitseigenschap van het getal 1.
Figuur 1:
Representatie van het optellen van twee vectoren A
en B. Het resultaat is de vector A+B.
|
|
Verder gelden de definities
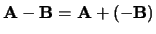 en
en
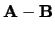 heet het verschil van
heet het verschil van  en
en 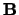 .
.




Next: Lineaire afhankelijkheid; ontbinden van
Up: Vectorrekening over de reële
Previous: Product van een scalar
Contents
Jo van den Brand
2004-09-25