



Next: Inwendig of scalair product
Up: Vectorrekening over de reële
Previous: Som en verschil van
Contents
De som
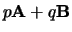 heet een lineaire combinatie van
heet een lineaire combinatie van  en
en 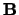 , terwijl
, terwijl
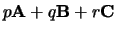 een lineaire
combinatie heet van
een lineaire
combinatie heet van  ,
, 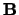 en
en 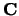 .
.
Definitie: een stelsel vectoren heet lineair onafhankelijk als
geen van die vectoren gelijk is aan een lineaire combinatie van andere
vectoren uit dat stelsel.
Stelling:  ,
, 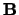 en
en 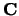 zijn lineair onafhankelijk
dan en slechts dan als uit
zijn lineair onafhankelijk
dan en slechts dan als uit
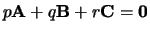 volgt
dat
volgt
dat 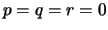 .
.
Als
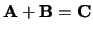 , dan heten
, dan heten  en
en 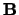 de
componenten van
de
componenten van 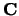 in de richtingen van
in de richtingen van  en
en 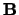 .
.
Als 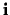 ,
, 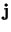 en
en 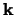 de eenheidsvectoren zijn in
de richtingen van de positieve
de eenheidsvectoren zijn in
de richtingen van de positieve  -,
-, 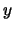 - en
- en 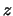 -as van een cartesiaans
coördinatenstelsel, dan is
-as van een cartesiaans
coördinatenstelsel, dan is
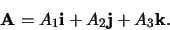 |
(1) |
Elke vector  is dus gelijk aan een lineaire combinatie van
de onderling lineair onafhankelijke vectoren
is dus gelijk aan een lineaire combinatie van
de onderling lineair onafhankelijke vectoren 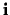 ,
, 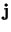 en
en 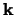 . De getallen
. De getallen 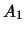 ,
, 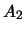 en
en 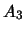 noemen we de kentallen
van
noemen we de kentallen
van  ten opzichte van de basis
ten opzichte van de basis
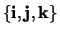 .
.
Figuur 2:
De vector 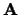 kan ontbonden worden in een lineaire combinatie van
de onderling lineair onafhankelijke vectoren
kan ontbonden worden in een lineaire combinatie van
de onderling lineair onafhankelijke vectoren 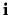 ,
, 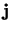 en
en 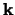 die een basis vormen.
die een basis vormen.
|
|
Blijkbaar geldt
-
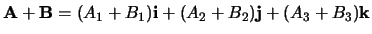 ,
,
-
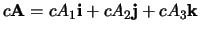 ,
,
-
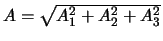 .
.




Next: Inwendig of scalair product
Up: Vectorrekening over de reële
Previous: Som en verschil van
Contents
Jo van den Brand
2004-09-25
![]() ,
, ![]() en
en ![]() zijn lineair onafhankelijk
dan en slechts dan als uit
zijn lineair onafhankelijk
dan en slechts dan als uit
![]() volgt
dat
volgt
dat ![]() .
.
![]() , dan heten
, dan heten ![]() en
en ![]() de
componenten van
de
componenten van ![]() in de richtingen van
in de richtingen van ![]() en
en ![]() .
.
![]() ,
, ![]() en
en ![]() de eenheidsvectoren zijn in
de richtingen van de positieve
de eenheidsvectoren zijn in
de richtingen van de positieve ![]() -,
-, ![]() - en
- en ![]() -as van een cartesiaans
coördinatenstelsel, dan is
-as van een cartesiaans
coördinatenstelsel, dan is
![\includegraphics[width=10cm]{Figures/basis.eps}](img111.png)