



Next: Matrix als transformatie-operator
Up: Matrixrekening
Previous: Determinant van een matrix
Contents
Definitie: Het product van een 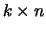 -matrix
-matrix  met
een
met
een 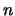 -dimensionale kolomvector
-dimensionale kolomvector 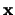 is gelijk aan de
is gelijk aan de 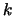 -dimensionale
kolomvector
-dimensionale
kolomvector 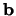 waarvan het
waarvan het 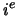 -element,
-element, 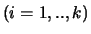 , gelijk
is aan het inwendig product van de
, gelijk
is aan het inwendig product van de 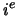 -rijvector van de matrix
-rijvector van de matrix  met de kolomvector
met de kolomvector 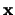 .
.
Dus als
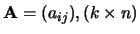 en
en
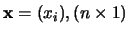 ,
dan is
,
dan is
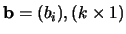 , waarbij
, waarbij
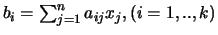 .
.
Het hele vergelijkingenstelsel van de paragraaf 6.2.1 kan dus genoteerd
worden als
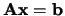 .
.
Jo van den Brand
2004-09-25
![]() en
en
![]() ,
dan is
,
dan is
![]() , waarbij
, waarbij
![]() .
.
![]() .
.