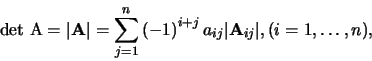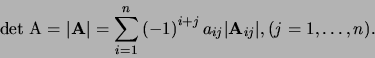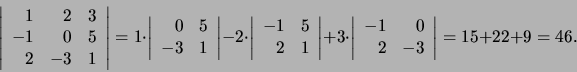Next: Product van een matrix
Up: Matrixrekening
Previous: Matrices
Contents
De determinant van de matrix
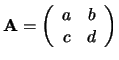 is het getal
is het getal
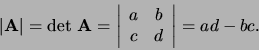 |
(228) |
De ondermatrix 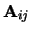 van de matrix
van de matrix  is de matrix
die ontstaat als uit
is de matrix
die ontstaat als uit  de
de 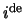 rij en de
rij en de 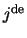 kolom weggelaten worden.
kolom weggelaten worden.
Voorbeeld: Als
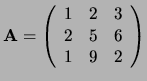 , dan is
, dan is
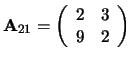 .
.
De determinant van de vierkante matrix
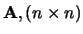 is het getal
is het getal
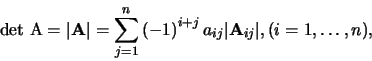 |
(229) |
en ook
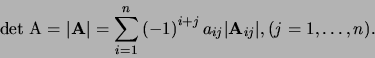 |
(230) |
Dit zijn de formules voor het ontwikkelen van det  volgens
de
volgens
de 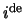 rij, respectievelijk volgens de
rij, respectievelijk volgens de 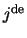 kolom.
kolom.
Voorbeeld: We ontwikkelen volgens de eerste rij.
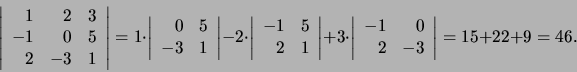 |
(231) |
Jo van den Brand
2004-09-25
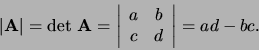
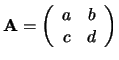 is het getal
is het getal
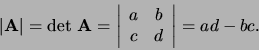
![]() van de matrix
van de matrix ![]() is de matrix
die ontstaat als uit
is de matrix
die ontstaat als uit ![]() de
de ![]() rij en de
rij en de ![]() kolom weggelaten worden.
kolom weggelaten worden.
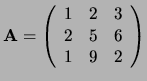 , dan is
, dan is
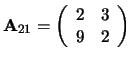 .
.
![]() is het getal
is het getal