



Next: Determinant van een matrix
Up: Matrixrekening
Previous: Matrixrekening
Contents
Matrices
Het stelsel van 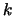 lineaire vergelijkingen met
lineaire vergelijkingen met 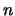 onbekenden
onbekenden
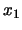 tot en met
tot en met 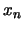 ,
,
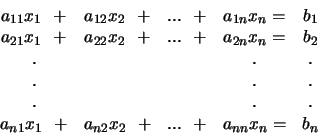 |
(225) |
is volkomen gekarakteriseerd door de getalverzamelingen
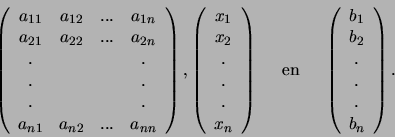 |
(226) |
Het eerste van deze getallenschema's heet een matrix van de orde k 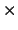 n;
deze matrix bevat namelijk
n;
deze matrix bevat namelijk 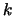 rijen en
rijen en 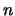 kolommen. De andere twee getalgroepen
zijn blijkbaar kolomvectoren, die ook opgevat kunnen worden als matrices van
de orde
kolommen. De andere twee getalgroepen
zijn blijkbaar kolomvectoren, die ook opgevat kunnen worden als matrices van
de orde 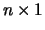 , respectievelijk
, respectievelijk 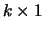 .
.
Definitie: Een matrix is een in rijen en kolommen gesorteerde
getalverzameling.
De getallen van die verzameling heten de elementen van de matrix.
Ze worden bij voorkeur met twee indices genoteerd, waarvan de eerste
het rangnummer van de rij en de tweede dat van de kolom aangeeft.
Als het aantal rijen 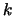 en het aantal kolommen
en het aantal kolommen 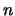 is dan heet
is dan heet
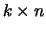 de orde van de matrix. Als
de orde van de matrix. Als 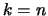 dan heet de matrix
een vierkante matrix van de orde
dan heet de matrix
een vierkante matrix van de orde 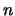 ofwel een
ofwel een 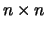 matrix.
matrix.
De matrix met elementen
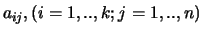 wordt
dan wel kortweg aangeduid met
wordt
dan wel kortweg aangeduid met
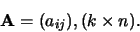 |
(227) |
Opmerkingen:
- Elke rij van een matrix is op zichzelf beschouwd een rijvector
en elke kolom van de matrix een kolomvector.
-
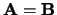 betekent dat
betekent dat  en
en 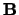 van
dezelfde orde,
van
dezelfde orde, 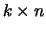 , zijn en dat
, zijn en dat
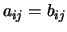 voor elke
voor elke
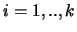 en elke
en elke 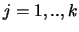 .
.




Next: Determinant van een matrix
Up: Matrixrekening
Previous: Matrixrekening
Contents
Jo van den Brand
2004-09-25
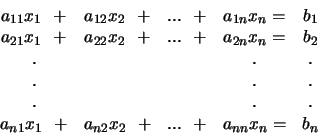
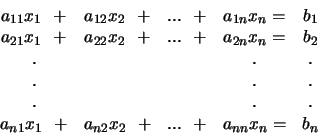

![]() en het aantal kolommen
en het aantal kolommen ![]() is dan heet
is dan heet
![]() de orde van de matrix. Als
de orde van de matrix. Als ![]() dan heet de matrix
een vierkante matrix van de orde
dan heet de matrix
een vierkante matrix van de orde ![]() ofwel een
ofwel een ![]() matrix.
matrix.
![]() wordt
dan wel kortweg aangeduid met
wordt
dan wel kortweg aangeduid met