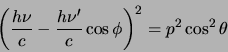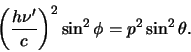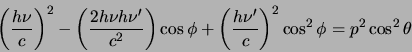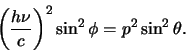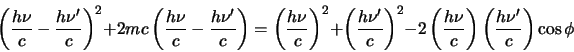Next: Waterstofatoom en Niels Bohr
Up: DEELTJES EN GOLVEN
Previous: Fotoelektrisch effect
Contents
In het Compton effect worden 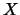 -ray fotonen (zogenaamde
Röntgenstralen) over een hoek
-ray fotonen (zogenaamde
Röntgenstralen) over een hoek 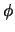 verstrooid aan vrije
elektronen. Hierdoor zal de golflengte van de fotonen toenemen
met het bedrag
verstrooid aan vrije
elektronen. Hierdoor zal de golflengte van de fotonen toenemen
met het bedrag
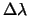 .
Deze Compton verschuiving wordt gegeven door
.
Deze Compton verschuiving wordt gegeven door
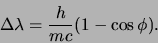 |
(83) |
Deze vergelijking volgt uit de wet van behoud van energie en
impuls als we het verstrooiingsproces beschrijven als een
billiardballen-achtige botsing tussen een foton en een vrij elektron.
Fig. 14 toont de data.
Figuur 14:
Meetresultaten van Compton voor vier waarden van de
verstrooiingshoek 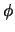 . Merk op dat de Compton verschuiving
. Merk op dat de Compton verschuiving
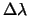 toeneemt met toenemende verstrooiingshoek.
toeneemt met toenemende verstrooiingshoek.
|
|
We kunnen de uitdrukking voor
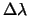 afleiden door
energie- en impulsbehoud te combineren. We beschouwen
Compton verstrooiing als een elastische botsing; zie Fig. 15.
afleiden door
energie- en impulsbehoud te combineren. We beschouwen
Compton verstrooiing als een elastische botsing; zie Fig. 15.
Figuur 15:
Compton verstrooiing van een foton aan een elektron kan worden
beschouwd als een elastische botsing.
|
|
Voor energiebehoud geldt
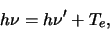 |
(84) |
waarbij 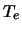 de kinetische
energie van het over een hoek
de kinetische
energie van het over een hoek 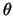 teruggestoten
elektron voorstelt.
Behoud van impuls geeft
teruggestoten
elektron voorstelt.
Behoud van impuls geeft
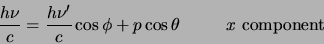 |
(85) |
en
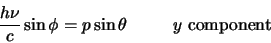 |
(86) |
met 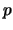 de impuls van het verstrooide elektron. Vervolgens kwadrateren
we beide vergelijkingen.
de impuls van het verstrooide elektron. Vervolgens kwadrateren
we beide vergelijkingen.
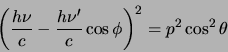 |
(87) |
en
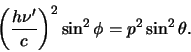 |
(88) |
We tellen nu beide vergelijkingen op en vinden
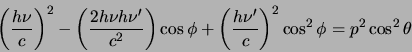 |
(89) |
en
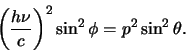 |
(90) |
Omdat
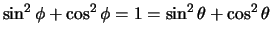 vinden we
vinden we
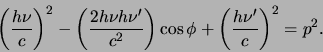 |
(91) |
Voor het elektron hebben we
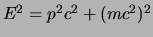 en als
en als 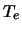 de
kinetische energie is, dan geldt
de
kinetische energie is, dan geldt
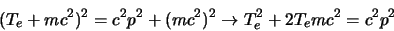 |
(92) |
of
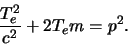 |
(93) |
Voor 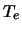 gebruiken we vergelijking (87) en voor
gebruiken we vergelijking (87) en voor 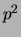 vergelijking (94) en vinden
vergelijking (94) en vinden
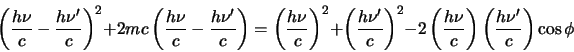 |
(94) |
en
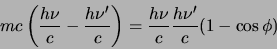 |
(95) |
en dus
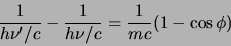 |
(96) |
Er geldt
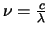 en
en
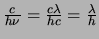 . We
vermenigvuldigen met
. We
vermenigvuldigen met 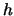 en vinden
en vinden
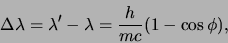 |
(97) |
waarbij
 m de zogenaamde
Compton golflengte is. De relatief eenvoudige aanname dat Compton
verstrooiing een elastische botsing is tussen een inkomend
foton en een bijna vrij atomair elektron, verklaart de experimentele
observatie van een toename in de golflengte, die onafhankelijk
is van de energie van het inkomend foton en de aard van
het materiaal. Met dit model kunnen we echter niet de relatieve
waarschijnlijkheid van Compton verstrooiing uitrekenen als
functie van de inkomende foton energie en de hoeken van het
verstrooide elektron en foton. Daartoe zouden we quantumveldentheorie
dienen toe te passen.
m de zogenaamde
Compton golflengte is. De relatief eenvoudige aanname dat Compton
verstrooiing een elastische botsing is tussen een inkomend
foton en een bijna vrij atomair elektron, verklaart de experimentele
observatie van een toename in de golflengte, die onafhankelijk
is van de energie van het inkomend foton en de aard van
het materiaal. Met dit model kunnen we echter niet de relatieve
waarschijnlijkheid van Compton verstrooiing uitrekenen als
functie van de inkomende foton energie en de hoeken van het
verstrooide elektron en foton. Daartoe zouden we quantumveldentheorie
dienen toe te passen.
Merk op dat zowel in de vergelijking van het fotoelektrisch effect
als het Compton effect de constante van Planck voorkomt. Deze
constante, alhoewel klein, is het bepalende kenmerk van de moderne
quantummechanica. De studie van de golflengteverdeling van de
straling die uitgezonden wordt door verwarmde zwarte lichamen,
gaf als eerste aanleiding tot het concept van energie quantisatie,
en hiermee werd de constante van Planck in de moderne fysica
geïntroduceerd.




Next: Waterstofatoom en Niels Bohr
Up: DEELTJES EN GOLVEN
Previous: Fotoelektrisch effect
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=5cm]{Figures/Fig4.eps}](img378.png)
![\includegraphics[width=10cm]{Figures/compton1.eps}](img379.png)