



Next: Sferisch harmonische functies
Up: IMPULSMOMENT
Previous: Operator voor impuls in
Contents
We zullen nu de operatoren voor het impulsmoment van een
deeltje nader beschouwen. We zien in vergelijking (538)
dat de componenten zijn opgebouwd uit commuterende Hermitische
operatoren. Daarom zal 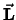 ook Hermitisch zijn.
In het algemeen geldt voor een commutator van de vorm
ook Hermitisch zijn.
In het algemeen geldt voor een commutator van de vorm
![$[a+b,c+d]$](img1552.png) de relatie
de relatie
![\begin{displaymath}
\begin{array}{ll}
[a+b,c+d] &=(a+b)(c+d) - (c+d)(a+b)
...
...d-db \\
& = [a,c] + [a,d] + [b,c] + [b,d] .\\
\end{array}
\end{displaymath}](img1553.png) |
(550) |
Hiermee vinden we de commutatierelaties voor de componenten
van het impulsmoment. Bijvoorbeeld
![\begin{displaymath}
\begin{array}{ll}
[ {\bf L_x},{\bf L_y} ] & =
[ {\bf y}{...
... y}{\bf p_x} ) \\
& =
i\hbar {\bf L_z} . \\
\end{array}
\end{displaymath}](img1554.png) |
(551) |
Op analoge wijze ontdekken we dat ook de overige componenten niet
commuteren. We vinden
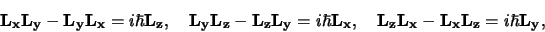 |
(552) |
We kunnen dit afkorten tot
![\begin{displaymath}
{\bf\vec L \times \vec L} = i\hbar{\bf\vec L},
{\rm of...
... als}
[{\bf L_i,L_j}] = i\hbar \epsilon_{ijk} {\bf L_k}.
\end{displaymath}](img1556.png) |
(553) |
Hierbij is
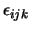 de volledig antisymmetrische tensor in
drie dimensies gegeven door
de volledig antisymmetrische tensor in
drie dimensies gegeven door
 |
(554) |
Dit betekent dat de componenten van het impulsmoment van een
deeltje niet allemaal op dezelfde tijd meetbaar zijn.
Vervolgens beschouwen de commutatierelaties met het kwadraat van het
impulsmoment.
![\begin{displaymath}
\begin{array}{ll}
[ {\bf L}^2,{\bf L_x} ]
& =
[ {\bf L...
...L_y} + i\hbar {\bf L_y}{\bf L_z} \\
& = 0. \\
\end{array}
\end{displaymath}](img1559.png) |
(555) |
Evenzo vinden we dat
![$[ {\bf L}^2,{\bf L_y} ] = [ {\bf L}^2,{\bf L_z} ] = 0$](img1560.png) .
De operator van
het kwadraat van het impulsmoment van een deeltje commuteert met
alle componenten van de operator van het impulsmoment. Er geldt
.
De operator van
het kwadraat van het impulsmoment van een deeltje commuteert met
alle componenten van de operator van het impulsmoment. Er geldt
![\begin{displaymath}[{\bf L}^2,{\bf L_x}]= [{\bf L}^2,{\bf L_y}] = [{\bf L}^2,{\bf L_z}] = 0.
\end{displaymath}](img1561.png) |
(556) |
Omdat 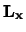 ,
, 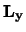 en
en 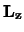 niet commuteren, kan slechts
een van deze operatoren een gezamelijke basis met
niet commuteren, kan slechts
een van deze operatoren een gezamelijke basis met 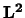 hebben, en
we kiezen hier
hebben, en
we kiezen hier 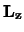 voor.
voor.




Next: Sferisch harmonische functies
Up: IMPULSMOMENT
Previous: Operator voor impuls in
Contents
Jo van den Brand
2004-09-25
![]() ook Hermitisch zijn.
In het algemeen geldt voor een commutator van de vorm
ook Hermitisch zijn.
In het algemeen geldt voor een commutator van de vorm
![]() de relatie
de relatie
![\begin{displaymath}
\begin{array}{ll}
[a+b,c+d] &=(a+b)(c+d) - (c+d)(a+b)
...
...d-db \\
& = [a,c] + [a,d] + [b,c] + [b,d] .\\
\end{array}
\end{displaymath}](img1553.png)
![\begin{displaymath}
\begin{array}{ll}
[ {\bf L_x},{\bf L_y} ] & =
[ {\bf y}{...
... y}{\bf p_x} ) \\
& =
i\hbar {\bf L_z} . \\
\end{array}
\end{displaymath}](img1554.png)

![\begin{displaymath}
\begin{array}{ll}
[ {\bf L}^2,{\bf L_x} ]
& =
[ {\bf L...
...L_y} + i\hbar {\bf L_y}{\bf L_z} \\
& = 0. \\
\end{array}
\end{displaymath}](img1559.png)