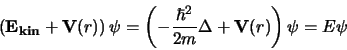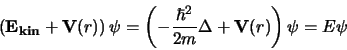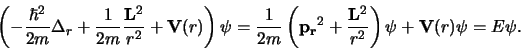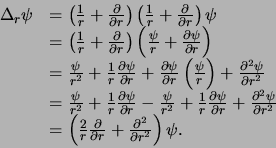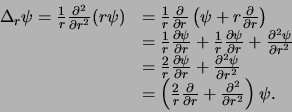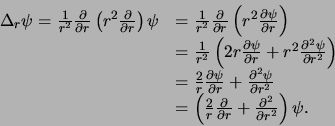Next: Commutatierelaties voor het impulsmoment
Up: IMPULSMOMENT
Previous: Inleiding
Contents
De Schrödingervergelijking kan geschreven worden als
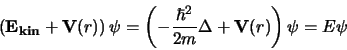 |
(544) |
en dus
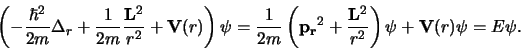 |
(545) |
Allereerst laten we zien dat met de definitie
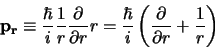 |
(546) |
voor de radiële impuls, we een uitdrukking voor de
radiële Laplace operator, 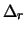 , krijgen die in overeenstemming
is met de uitdrukking gegeven in vergelijking (430).
, krijgen die in overeenstemming
is met de uitdrukking gegeven in vergelijking (430).
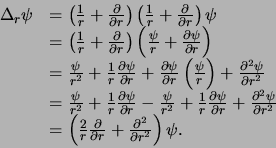 |
(547) |
Ook geldt dat
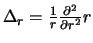 .
Het bewijs gaat als volgt
.
Het bewijs gaat als volgt
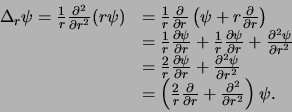 |
(548) |
Tenslotte geldt ook
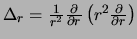 .
Dit laatste bewijs gaat als volgt
.
Dit laatste bewijs gaat als volgt
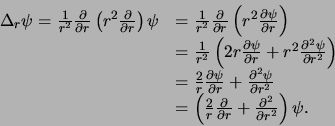 |
(549) |




Next: Commutatierelaties voor het impulsmoment
Up: IMPULSMOMENT
Previous: Inleiding
Contents
Jo van den Brand
2004-09-25