



Next: Lineaire afbeeldingen
Up: Lineaire ruimten en lineaire
Previous: Lineaire onafhankelijkheid, basis, dimensie
Contents
Definitie: Een inwendig product binnen een vectorruimte 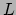 is een afbeelding van
is een afbeelding van
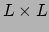 naar
naar
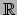 , waarvoor, als
, waarvoor, als
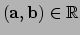 het aan
het aan
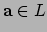 en
en
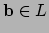 toegevoegde getal is, geldt
toegevoegde getal is, geldt
-
![$ \forall_{{\bf a},{\bf b} \in L}
[ ({\bf a},{\bf b}) = ({\bf b}, {\bf a}) ]$](img1912.png)
-
![$ \forall_{{\bf a},{\bf b},{\bf c} \in L}
[ ({\bf a},{\bf b} + {\bf c} ) = ({\bf a},{\bf b})+({\bf a}, {\bf c}) ]$](img1913.png)
-
![$ \forall_{{\bf a},{\bf b} \in L, p \in {\mathbb{R}}}
[ (p{\bf a},{\bf b}) = p({\bf a}, {\bf b}) ]$](img1914.png)
-
![$ \forall_{{\bf a} \in L}
[ ({\bf a},{\bf a}) \geq 0 ]; ({\bf a},{\bf0}) = 0$](img1915.png)
Het getal
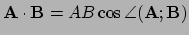 zullen we `het' inwendig product in
zullen we `het' inwendig product in 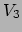 noemen. Met `het' inwendig
product in
noemen. Met `het' inwendig
product in
 duiden we aan
duiden we aan
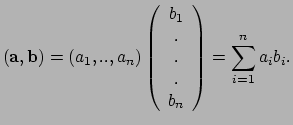 |
(439) |
Dit inwendig product noteren we dus door de eerste vector als rijvector
en de tweede als kolomvector te schrijven.
Definitie: De norm
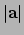 van de vector
van de vector 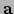 is het getal
is het getal
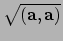 .
.
Definitie: De vectoren 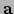 en
en 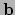 zijn onderling
orthogonaal dan en slechts dan als
zijn onderling
orthogonaal dan en slechts dan als
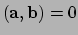 .
.
Jo van den Brand
2009-01-31
![]() is een afbeelding van
is een afbeelding van
![]() naar
naar
![]() , waarvoor, als
, waarvoor, als
![]() het aan
het aan
![]() en
en
![]() toegevoegde getal is, geldt
toegevoegde getal is, geldt
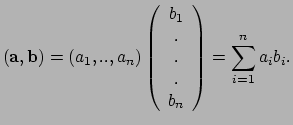
![]() van de vector
van de vector ![]() is het getal
is het getal
![]() .
.
![]() en
en ![]() zijn onderling
orthogonaal dan en slechts dan als
zijn onderling
orthogonaal dan en slechts dan als
![]() .
.