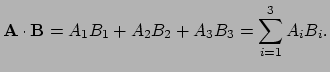Next: Voorbeelden
Up: Vectorrekening over de reële
Previous: Lineaire afhankelijkheid; ontbinden van
Contents
Definitie
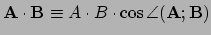 |
(431) |
Het inwendig product van vectoren is dus een scalar.
Eigenschappen
-
![$ \forall_{{\bf A},{\bf B}} [ {\bf A} \cdot {\bf B} = {\bf B} \cdot {\bf A} ]$](img1853.png) commutatieve eigenschap
commutatieve eigenschap
-
![$ \forall_{{\bf A},{\bf B},{\bf C}} [ {\bf A} \cdot ({\bf B} + {\bf C})
= {\bf A} \cdot {\bf B} + {\bf A} \cdot {\bf C} ]$](img1854.png) distributieve eigenschap
distributieve eigenschap
Uit de definitie volgt
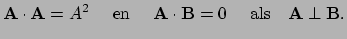 |
(432) |
Dus ook
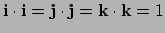 en
en
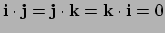 en dus
en dus
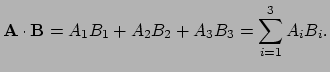 |
(433) |
Merk op dat als
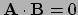 , dan is
, dan is 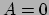 of
of 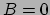 of
of
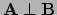 .
.
Jo van den Brand
2009-01-31
![]() en
en
![]() en dus
en dus