In de mechanica willen we de banen van deeltjes (of meer algemeen objecten, dat
wil zeggen verzamelingen van deeljes) beschrijven. Om een dergelijke beschrijving
mogelijk te maken kiezen we een willekeurig coördinatenstelsel in de
drie-dimensionale (3D) ruimte. Dit stelsel bevat een oorsprong en drie veelal
onderling loodrecht gekozen richtingen die we vervolgens de ![]() ,
, ![]() en
en
![]() -richting noemen en aangeven met respectievelijk de
vectoren
-richting noemen en aangeven met respectievelijk de
vectoren ![]() ,
, ![]() en
en ![]() . Verder brengen we een afstandsverdeling
aan op de
. Verder brengen we een afstandsverdeling
aan op de ![]() ,
, ![]() en
en ![]() -as. Tijd wordt gemeten met een universeel lopende
klok en een willekeurig tijdstip wordt gekozen als
-as. Tijd wordt gemeten met een universeel lopende
klok en een willekeurig tijdstip wordt gekozen als ![]() . Vervolgens worden
tijden van gebeurtenissen relatief gemeten ten opzichte van
. Vervolgens worden
tijden van gebeurtenissen relatief gemeten ten opzichte van ![]() .
.
We beschrijven de positie waarop een object zich bevindt in de
3D ruimte met de plaatsvector (of positievector)
| (1) |
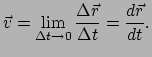 |
(2) |
De instantane versnelling ![]() is ook een vector en is de mate van verandering
van de snelheidsvector. Er geldt
is ook een vector en is de mate van verandering
van de snelheidsvector. Er geldt
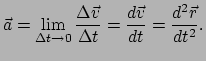 |
(3) |