Cilindirische coördinaten

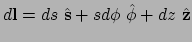$d{\bf l} = ds ~ \hat {\bf s} + s d\phi ~ \hat {\bf\phi} + dz ~ \hat {\bf z}$ lijn-element

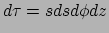$d\tau = sds d\phi dz$ volume-element

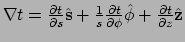$\nabla t = {\partial t \over \partial s} \hat {\bf s} + {1 \over s}{\partial ... ...ver \partial \phi} \hat {\bf\phi} + {\partial t \over \partial z} \hat {\bf z}$ gradiënt

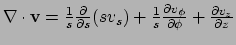$\nabla \cdot {\bf v} = {1 \over s}{\partial \over \partial s}(s v_s) + {1 \over s}{\partial v_\phi \over \partial \phi} + {\partial v_z \over \partial z}$ divergentie

$\nabla \times {\bf v} = \left[ {1 \over s}{\partial v_z \over \partial \phi} ... ...partial s}(sv_\phi ) - {\partial v_s \over \partial \phi} \right] \hat {\bf z}$ rotatie

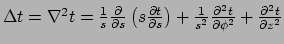$\Delta t = \nabla^2 t = {1 \over s}{\partial \over \partial s} \left( s {\par... ...r s^2}{\partial^2 t \over \partial \phi^2} + {\partial^2 t \over \partial z^2}$ Laplace operator

FUNDAMENTELE THEOREMAS

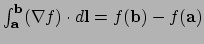$\int_{\bf a}^{\bf b} (\nabla f) \cdot d{\bf l} = f({\bf b}) - f({\bf a})$ Gradiënt theorema

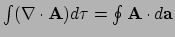$\int (\nabla \cdot {\bf A} ) d\tau = \oint {\bf A} \cdot d{\bf a}$ Divergentie theorema (stelling van Gauss)

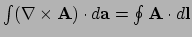$\int (\nabla \times {\bf A} ) \cdot d{\bf a} = \oint {\bf A} \cdot d{\bf l}$ Rotatie theorema (stelling van Stokes)