


Next: APPENDIX A: Relativistische Kinematica
Up: HADRON STRUCTUUR
Previous: Diepinelastische Verstrooiing
Elektron - Positron Annihilatie
De reactie
heeft duidelijk
aanwijzingen gegeven voor het bestaan van gluonen en het
quantumgetal kleur. Het is mogelijk dat in het eindkanaal hadronen
worden geproduceerd en hiermee kan dan het mechanisme van
jet-productie worden bestudeerd. Het basis idee is weergegeven in
fig. 69.
Figure 69:
Basis mechanisme voor twee-jet productie in elektron-positron
annihilatie.
|
De reactie verloopt in twee stappen: een primair elektromagnetisch
proces,
leidt tot de productie van een quark-antiquark paar. Dit wordt gevolgd
door een proces uit de sterke wisselwerking, genoemd fragmentatie,
waarbij het hoge energie paar wordt geconverteerd in twee
jets van hadronen. Deze jets zullen in het zwaartepuntsysteem
in tegenovergestelde richtingen worden geëmitteerd, zoals vereist
door impulsbehoud.
Een ander mogelijk proces is
.
Dit mechanisme is identiek aan dat van quark-paar productie en
beide reacties zijn nauw aan elkaar verwant. De differentiële
werkzame doorsnede wordt gegeven door
waarbij de productiehoek is van een muon ten opzichte van
het inkomende elektron in het zwaartepuntsysteem. De analoge
werkzame doorsnede voor quark-antiquark paarproductie van
paren van een bepaald type wordt verkregen
door de muon lading 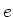 te vervangen door de quarklading .
Omdat de lading hetzelfde is voor de drie kleurtoestanden
te vervangen door de quarklading .
Omdat de lading hetzelfde is voor de drie kleurtoestanden 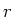 ,
en
,
en 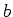 , dienen we nog te vermenigvuldigen met om de
drie kleurtoestanden , en in
rekening te brengen. We vinden
, dienen we nog te vermenigvuldigen met om de
drie kleurtoestanden , en in
rekening te brengen. We vinden
Figure:
Vergelijking van de hoekverdeling van twee-jet gebeurtenissen,
verkregen met het elektron-positron annihilatie experiment van de CELLO
collaboratie te DESY, met de theoretisch verspelde
afhankelijkheid.
|
De hoekverdeling van de jets dient evenredig te zijn met
en fig. 70 laat zien dat dit
inderdaad het geval is.
Terwijl twee-jet productie dominant is, verwachten we dat er soms
door een van de geproduceerde quarks een gluon wordt uitgezonden
met een relatief hoge impuls. Dit proces wordt gluon
bremsstrahlung genoemd en leidt tot de formatie
van zogenaamde drie-jet gebeurtenissen. Zulke reacties zijn
inderdaad geobserveerd en leveren sterke aanwijzingen voor de
realiteit van de spin-1 gluonen, waarvan het bestaan wordt aangenomen door QCD.
De analyse van de meetgegevens is verre van triviaal, omdat het
niet duidelijk is welke van de jets bij het gluon hoort.
Gedetailleerde berekeningen laten zien dat de kinematische
verdelingen gevoelig zijn voor de spin van het gluon. De gemeten
verdelingen worden vergeleken met theoretische verwachtingen die
gebaseerd zijn op spin-0 en spin-1 gluonen.
Fig. 71 toont dat spin-1 voor de gluonen een
duidelijk voorkeur geniet.
Figure:
Hoekverdeling van drie-jet gebeurtenissen zoals gemeten door
de TASSO collaboratie. De hoek 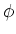 wordt besproken in de
tekst. De gestreepte en getrokken curven tonen respectievelijk de theoretische
voorspellingen voor spin-0 en spin-1 gluonen (Uit S.-L Wu,
Physics Reports 107, 59 (1984)).
wordt besproken in de
tekst. De gestreepte en getrokken curven tonen respectievelijk de theoretische
voorspellingen voor spin-0 en spin-1 gluonen (Uit S.-L Wu,
Physics Reports 107, 59 (1984)).
|
De jets worden geklassificeerd aan de hand van hun energie,
, in het gemeenschappelijke zwaartepuntsysteem. De hoekverdeling
is geplot voor jet 1 als functie van de hoek 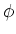 tussen de richting
van jet 1 en de gezamelijke vluchtrichting van jets 2 en 3.
De waarschijnlijkheid dat een quark een gluon uitzendt wordt bepaald
door de sterke koppelingsconstante . De gemeten
telsnelheid voor drie-jet gebeurtenissen kan dus gebruikt worden om de
waarde van te bepalen. De analyse is uitermate complex
en levert de waarde
voor experimenten
met een totale zwaartepuntsenergie in het
gebied 30 - 40 GeV.
tussen de richting
van jet 1 en de gezamelijke vluchtrichting van jets 2 en 3.
De waarschijnlijkheid dat een quark een gluon uitzendt wordt bepaald
door de sterke koppelingsconstante . De gemeten
telsnelheid voor drie-jet gebeurtenissen kan dus gebruikt worden om de
waarde van te bepalen. De analyse is uitermate complex
en levert de waarde
voor experimenten
met een totale zwaartepuntsenergie in het
gebied 30 - 40 GeV.
Figure:
Meetresultaten voor de verhouding
, waarbij de annihilatie
plaatsvindt via één foton of via de 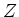 uitwisseling.
uitwisseling.
|
De gemeten waarden voor de totale werkzame doorsnede voor
elektron-positron annihilatie met hadronen in de eindtoestand
worden getoond in fig. 72. De figuur geeft de verhouding
waarbij de differentiële werkzame doorsnede is geïntegreerd
over de hoek .
De totale werkzame doorsnede is de som voor de quarks met type 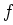 ,
die kunnen worden geproduceerd in de reactie met zwaartepuntsenergie
.
We kunnen dus schrijven
, waarbij de som
loopt over de quarks die bij een bepaalde energie geproduceerd
kunnen worden. Het aantal kleuren wordt aangegeven met (volgens
QCD geldt er ). Bij lage energieën, waar enkel de
,
die kunnen worden geproduceerd in de reactie met zwaartepuntsenergie
.
We kunnen dus schrijven
, waarbij de som
loopt over de quarks die bij een bepaalde energie geproduceerd
kunnen worden. Het aantal kleuren wordt aangegeven met (volgens
QCD geldt er ). Bij lage energieën, waar enkel de 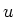 ,
, 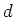 en
en 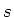 quarks gemaakt kunnen worden, verwachten we
quarks gemaakt kunnen worden, verwachten we
Boven de drempel voor productie (bij ongeveer 3 GeV),
maar onder de drempel voor productie, verwachten we
en boven de drempel voor vinden we
.
Fig. 72 geeft de gemeten waarden van de verhouding
als functie van de zwaartepuntsenergie . We zien duidelijk
de sprong van 2 naar bij
GeV. Ook
de sprong bij de drempel is zichtbaar. Het is duidelijk
dat deze data het bestaan van het quantumgetal kleur demonstreren.
Voor zeer hoge waarden van de zwaartepuntsenergie begint de zwakke
wisselwerking een rol te spelen, hetgeen een toename van tot
gevolg heeft.



Next: APPENDIX A: Relativistische Kinematica
Up: HADRON STRUCTUUR
Previous: Diepinelastische Verstrooiing
Jo van den Brand
2002-03-25
![]() tussen de richting
van jet 1 en de gezamelijke vluchtrichting van jets 2 en 3.
De waarschijnlijkheid dat een quark een gluon uitzendt wordt bepaald
door de sterke koppelingsconstante . De gemeten
telsnelheid voor drie-jet gebeurtenissen kan dus gebruikt worden om de
waarde van te bepalen. De analyse is uitermate complex
en levert de waarde
voor experimenten
met een totale zwaartepuntsenergie in het
gebied 30 - 40 GeV.
tussen de richting
van jet 1 en de gezamelijke vluchtrichting van jets 2 en 3.
De waarschijnlijkheid dat een quark een gluon uitzendt wordt bepaald
door de sterke koppelingsconstante . De gemeten
telsnelheid voor drie-jet gebeurtenissen kan dus gebruikt worden om de
waarde van te bepalen. De analyse is uitermate complex
en levert de waarde
voor experimenten
met een totale zwaartepuntsenergie in het
gebied 30 - 40 GeV.