



Next: WATERSTOFATOOM
Up: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Previous: Tijdevolutie van een systeem
Contents
Allereerst beschouwen we een systeem van twee deeltjes die
geen interactie met elkaar hebben. We kunnen de Hamiltoniaan
schrijven als
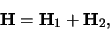 |
(405) |
waarbij 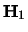 en
en 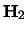 de Hamiltonianen zijn voor
deeltje 1 en 2. We kunnen nu de eigenfuncties en eigenwaarden
van de operator gegeven in vergelijking (411), schrijven
in termen van de één-deeltjes Hamiltonianen
de Hamiltonianen zijn voor
deeltje 1 en 2. We kunnen nu de eigenfuncties en eigenwaarden
van de operator gegeven in vergelijking (411), schrijven
in termen van de één-deeltjes Hamiltonianen 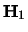 en
en 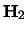 .
Er geldt
.
Er geldt
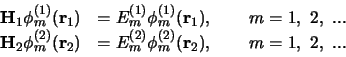 |
(406) |
met
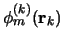 en
en
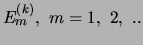 de eigenfuncties en eigenwaarden van de Hamiltoniaan
de eigenfuncties en eigenwaarden van de Hamiltoniaan 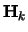 voor het deeltje met label
voor het deeltje met label 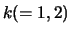 . Hieruit volgt dat voor
elk product van eigenfuncties
. Hieruit volgt dat voor
elk product van eigenfuncties
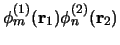 geldt dat
geldt dat
en dat de productfunctie
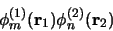 |
(407) |
een eigenfunctie is
van de Hamiltoniaan
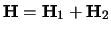 behorend bij
de eigenwaarde
behorend bij
de eigenwaarde
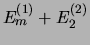 . We vinden dat voor een
systeem van twee niet-wisselwerkende deeltjes de energie gegeven
wordt door de som van de energieën van de individuele deeltjes.
. We vinden dat voor een
systeem van twee niet-wisselwerkende deeltjes de energie gegeven
wordt door de som van de energieën van de individuele deeltjes.
De generalisatie van deze resultaten naar die van een systeem met
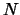 deeltjes zonder interactie, met een Hamiltoniaan
deeltjes zonder interactie, met een Hamiltoniaan
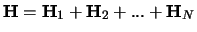 is triviaal.
In realistische gevallen, waarbij de
is triviaal.
In realistische gevallen, waarbij de 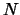 deeltjes wisselwerken, dienen
we termen toe te voegen aan de Hamiltoniaan die deze wisselwerking
tussen de deeltjes vertegenwoordigen. Hierdoor wordt het in het algemeen
moeilijk om de bijbehorende Schrödingervergelijking op te lossen.
Men gaat dan over tot benaderingsmethoden, storingsrekening,
symmetriebeschouwingen en/of numerieke methoden teneinde oplossingen te vinden.
deeltjes wisselwerken, dienen
we termen toe te voegen aan de Hamiltoniaan die deze wisselwerking
tussen de deeltjes vertegenwoordigen. Hierdoor wordt het in het algemeen
moeilijk om de bijbehorende Schrödingervergelijking op te lossen.
Men gaat dan over tot benaderingsmethoden, storingsrekening,
symmetriebeschouwingen en/of numerieke methoden teneinde oplossingen te vinden.




Next: WATERSTOFATOOM
Up: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Previous: Tijdevolutie van een systeem
Contents
Jo van den Brand
2004-09-25
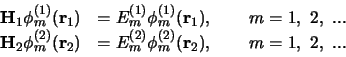
![]() deeltjes zonder interactie, met een Hamiltoniaan
deeltjes zonder interactie, met een Hamiltoniaan
![]() is triviaal.
In realistische gevallen, waarbij de
is triviaal.
In realistische gevallen, waarbij de ![]() deeltjes wisselwerken, dienen
we termen toe te voegen aan de Hamiltoniaan die deze wisselwerking
tussen de deeltjes vertegenwoordigen. Hierdoor wordt het in het algemeen
moeilijk om de bijbehorende Schrödingervergelijking op te lossen.
Men gaat dan over tot benaderingsmethoden, storingsrekening,
symmetriebeschouwingen en/of numerieke methoden teneinde oplossingen te vinden.
deeltjes wisselwerken, dienen
we termen toe te voegen aan de Hamiltoniaan die deze wisselwerking
tussen de deeltjes vertegenwoordigen. Hierdoor wordt het in het algemeen
moeilijk om de bijbehorende Schrödingervergelijking op te lossen.
Men gaat dan over tot benaderingsmethoden, storingsrekening,
symmetriebeschouwingen en/of numerieke methoden teneinde oplossingen te vinden.