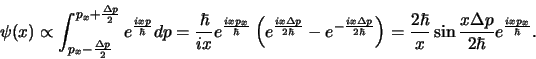Next: Schrödingervergelijking als eigenwaardenvergelijking
Up: Grondslagen van de quantummechanica
Previous: Operatoren voor plaats en
Contents
Het is duidelijk dat een eigenfunctie van impuls (een harmonische golf)
niet tegelijkertijd een eigenfunctie van de plaats (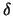 -functie)
kan zijn. Er bestaat dus geen toestand, waarin een deeltje tegelijkertijd
een scherp bepaalde impuls
-functie)
kan zijn. Er bestaat dus geen toestand, waarin een deeltje tegelijkertijd
een scherp bepaalde impuls 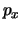 en een scherp bepaalde positie
en een scherp bepaalde positie  heeft. Men kan zelfs zeggen dat voor een toestand met scherp bepaalde
impuls de positie volledig onbepaald is en omgekeerd.
Een voorwaarde voor het bestaan van een verwachtingswaarde van de
plaats is dat de golffunctie
heeft. Men kan zelfs zeggen dat voor een toestand met scherp bepaalde
impuls de positie volledig onbepaald is en omgekeerd.
Een voorwaarde voor het bestaan van een verwachtingswaarde van de
plaats is dat de golffunctie 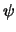 van het deeltje ergens (of op
meerdere plaatsen) geconcentreerd is. Voor het bestaan van de
verwachtingswaarde van de impuls, dient deze op zijn minst een
golfkarakter te hebben. Een redelijk compromis wordt bijvoorbeeld
gegeven door de functie in Fig. 32.
van het deeltje ergens (of op
meerdere plaatsen) geconcentreerd is. Voor het bestaan van de
verwachtingswaarde van de impuls, dient deze op zijn minst een
golfkarakter te hebben. Een redelijk compromis wordt bijvoorbeeld
gegeven door de functie in Fig. 32.
Figuur 32:
Superpositie van golven die gekozen zijn uit een
nauw golflengtegebied levert een golffunctie met een niet al te grote
spreiding in positie.
|
|
Een dergelijk golfpakket kan volgens de Fourieranalyse worden
opgebouwd uit een
groot aantal vlakke golven van de vorm (355), echter met
verschillende waarden voor 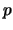 , dus met verschillende golflengten.
Deze impulsen dienen in een bepaald gebied
, dus met verschillende golflengten.
Deze impulsen dienen in een bepaald gebied 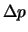 te liggen
en men dient er dan verder nog voor te zorgen dat de fasen zó
gekozen zijn dat men een maximum creëert op de positie
te liggen
en men dient er dan verder nog voor te zorgen dat de fasen zó
gekozen zijn dat men een maximum creëert op de positie 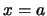 .
Op alle andere plaatsen kloppen de fasen dan niet meer, indien men
oneindig veel waarden voor
.
Op alle andere plaatsen kloppen de fasen dan niet meer, indien men
oneindig veel waarden voor 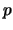 gebruikt (in geval van een eindig aantal
gebruikt (in geval van een eindig aantal
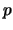 -waarden krijgen we periodieke herhalingen). We hebben in paragraaf
2.3.4 getoond,
dat een dergelijke superpositie een breedte
-waarden krijgen we periodieke herhalingen). We hebben in paragraaf
2.3.4 getoond,
dat een dergelijke superpositie een breedte 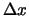 heeft, die met
de breedte van het gebruikte golflengtegebied samenhangt volgens
heeft, die met
de breedte van het gebruikte golflengtegebied samenhangt volgens
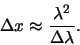 |
(357) |
Volgens de relatie van de Broglie is dat identiek aan
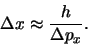 |
(358) |
Dit is de onzekerheidsrelatie van Heisenberg.
We zullen nu bovenstaande relatie afleiden voor het geval dat de gewenste
positie van het deeltje 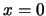 , de gemiddelde impuls
, de gemiddelde impuls 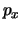 , en het
voor de superpositie gebruikte impulsgebied gelijk is aan
, en het
voor de superpositie gebruikte impulsgebied gelijk is aan
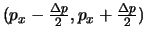 . Al deze
partiële golven zijn vertegenwoordigd met gelijke amplitude. Dus
met andere woorden: we weten niet welke impulswaarde uit dit gebied
een voorkeur heeft, maar enkel dat de impuls in dit gebied ligt. Alle
waarden in dit gebied zijn even waarschijnlijk! We vinden de
toestandsfunctie door superpositie en integreren dus over alle partiële
golven,
. Al deze
partiële golven zijn vertegenwoordigd met gelijke amplitude. Dus
met andere woorden: we weten niet welke impulswaarde uit dit gebied
een voorkeur heeft, maar enkel dat de impuls in dit gebied ligt. Alle
waarden in dit gebied zijn even waarschijnlijk! We vinden de
toestandsfunctie door superpositie en integreren dus over alle partiële
golven,
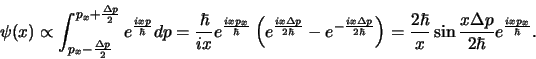 |
(359) |
Dit is een vlakke golf, waarvan de amplitude met de factor
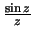 gemoduleerd is (
gemoduleerd is (
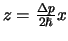 ). Deze functie heeft precies
de vorm zoals getoond in Fig. 32. Het hoofdmaximum ligt tussen
de waarden
). Deze functie heeft precies
de vorm zoals getoond in Fig. 32. Het hoofdmaximum ligt tussen
de waarden
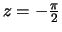 en
en
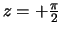 en heeft een breedte
en heeft een breedte
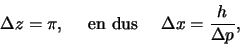 |
(360) |
waaruit de onzekerheidsrelatie van Heisenberg volgt.
Als we de operatoren beschouwen, dan uit zich de onzekerheidsrelatie
in het feit dat de plaats- en impulsoperator niet verwisselbaar zijn.
Men krijgt verschillende resultaten als men op een functie eerst de
plaats- en dan de impulsoperator laat werken of omgekeerd,
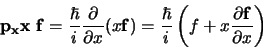 |
(361) |
en
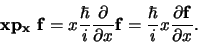 |
(362) |
Het verschil van beide uitdrukkingen bedraagt
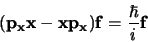 |
(363) |
en toont dat iedere functie een eigenfunctie is van de operator
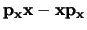 met een eigenwaarde gelijk aan
met een eigenwaarde gelijk aan 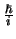 .
We gebruiken voor het operatorverschil de notatie
.
We gebruiken voor het operatorverschil de notatie
![$\left[ {\bf p_x},{\bf x} \right] = {\bf p_x x} - {\bf xp_x}$](img1160.png) en noemen
en noemen
![$\left[ {\bf p_x},{\bf x} \right]$](img1161.png) de commutator van
de commutator van 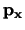 en
en
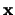 . Onafhankelijk van de keuze van
. Onafhankelijk van de keuze van 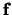 kan men dus de zuivere
operatorvergelijking
kan men dus de zuivere
operatorvergelijking
![\begin{displaymath}[ {\bf p_x},{\bf x} ]= {\bf p_x x} - {\bf xp_x} = {\hbar \over i}
\end{displaymath}](img1163.png) |
(364) |
opschrijven. Dit is een van de verwisselingsrelaties.
Wat de impuls betreft zijn er natuurlijk drie, voor
elke coördinaat één. Ook bestaat er een dergelijke relatie
tussen energie en tijd. Ze geven de abstracte voorstelling van
de onzekerheidsrelaties, die gewoonlijk als volgt geformuleerd
wordt: `Het is onmogelijk de plaats en impuls van een deeltje
of het tijdstip en energie van een gebeurtenis, in het algemeen een
paar geconjugeerde grootheden tegelijkertijd scherp te bepalen.
Bij een dergelijke meting resteren er altijd onzekerheden 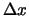 en
en 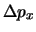 , respectievelijk
, respectievelijk 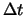 en
en 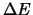 , waarvan
het product principieel niet kleiner gemaakt kan worden
dan
, waarvan
het product principieel niet kleiner gemaakt kan worden
dan 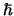 .'
.'




Next: Schrödingervergelijking als eigenwaardenvergelijking
Up: Grondslagen van de quantummechanica
Previous: Operatoren voor plaats en
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=14cm]{Figures/Fig9.eps}](img1143.png)
![\includegraphics[width=14cm]{Figures/Fig9.eps}](img1143.png)
![]() , de gemiddelde impuls
, de gemiddelde impuls ![]() , en het
voor de superpositie gebruikte impulsgebied gelijk is aan
, en het
voor de superpositie gebruikte impulsgebied gelijk is aan
![]() . Al deze
partiële golven zijn vertegenwoordigd met gelijke amplitude. Dus
met andere woorden: we weten niet welke impulswaarde uit dit gebied
een voorkeur heeft, maar enkel dat de impuls in dit gebied ligt. Alle
waarden in dit gebied zijn even waarschijnlijk! We vinden de
toestandsfunctie door superpositie en integreren dus over alle partiële
golven,
. Al deze
partiële golven zijn vertegenwoordigd met gelijke amplitude. Dus
met andere woorden: we weten niet welke impulswaarde uit dit gebied
een voorkeur heeft, maar enkel dat de impuls in dit gebied ligt. Alle
waarden in dit gebied zijn even waarschijnlijk! We vinden de
toestandsfunctie door superpositie en integreren dus over alle partiële
golven,