



Next: Product van matrices
Up: Matrixrekening
Previous: Som van matrices
Contents
Als
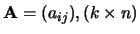 , dan is
, dan is
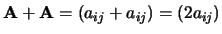 . Deze matrix
van orde
. Deze matrix
van orde 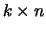 noemen we
noemen we 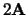 . Analoog kan het
product van een matrix met een willekeurige scalar gedefinieerd
worden als
. Analoog kan het
product van een matrix met een willekeurige scalar gedefinieerd
worden als
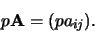 |
(236) |
Zowel ten opzichte van optellen van matrices als van scalaren is
deze vermenigvuldiging distributief,
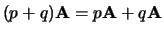 en
en
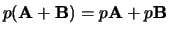 . Bovendien geldt
de associatieve eigenschap
. Bovendien geldt
de associatieve eigenschap
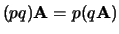 , terwijl
kennelijk
, terwijl
kennelijk
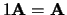 .
.
Samenvattend concluderen we dat de verzameling van matrices
van een bepaalde orde een lineaire ruimte is.
Jo van den Brand
2004-09-25