



Next: Fourieranalyse van golfverschijnselen
Up: KLASSIEKE GOLFVERSCHIJNSELEN
Previous: Inleiding
Contents
Een fysische situatie die zich zonder vervorming voortplant
langs de  -as wordt een golfbeweging genoemd en wordt
beschreven door de uitdrukking
-as wordt een golfbeweging genoemd en wordt
beschreven door de uitdrukking
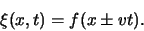 |
(33) |
Men noemt 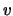 de fasesnelheid en als
de fasesnelheid en als 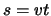 , waarin
, waarin 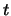 de tijd voorstelt, dan is de vervorming over een afstand
de tijd voorstelt, dan is de vervorming over een afstand
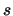 naar links opgeschoven (zie Fig. 6).
De grootheid
naar links opgeschoven (zie Fig. 6).
De grootheid 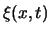 kan een verscheidenheid aan observabelen
voorstellen, zoals de druk in een gas, transversale uitwijking
van een snaar.
kan een verscheidenheid aan observabelen
voorstellen, zoals de druk in een gas, transversale uitwijking
van een snaar.
Figuur 6:
Representatie van een fysische situatie die zich zonder
vervorming voortplant langs de  -as.
-as.
|
|
Een bijzonder geval treedt op als 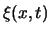 een sinusfunctie
of harmonische functie is, zoals
een sinusfunctie
of harmonische functie is, zoals
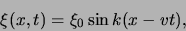 |
(34) |
waarbij 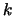 het golfgetal wordt genoemd. Als we
het golfgetal wordt genoemd. Als we  vervangen door
vervangen door
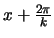 krijgen we voor
krijgen we voor 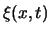 weer dezelfde waarde, namelijk
weer dezelfde waarde, namelijk
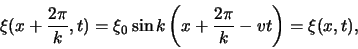 |
(35) |
met
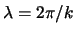 de golflengte van de kromme. We
kunnen vergelijking (34) ook schrijven als
de golflengte van de kromme. We
kunnen vergelijking (34) ook schrijven als
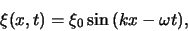 |
(36) |
waarin
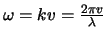 de cirkelfrequentie
van de golf voorstelt. Omdat
de cirkelfrequentie
van de golf voorstelt. Omdat
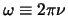 , met
, met 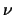 de frequentie, vinden we de belangrijke relatie
de frequentie, vinden we de belangrijke relatie
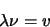 |
(37) |
tussen golflengte, frequentie en fasesnelheid.
Als 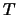 de periode van de trilling in elk punt is, kunnen
we vergelijking (34) ook schrijven als
de periode van de trilling in elk punt is, kunnen
we vergelijking (34) ook schrijven als
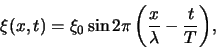 |
(38) |
Men kan gemakkelijk nagaan dat de algemene uitdrukking voor een
lopende golf geschreven kan worden als
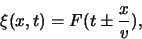 |
(39) |
waarin het positieve teken beantwoordt aan een voortplanting in de negatieve
 -richting en het minteken aan een voorplanting in positieve
-richting en het minteken aan een voorplanting in positieve  -richting.
Voor een harmonische golf kunnen we ook schrijven
-richting.
Voor een harmonische golf kunnen we ook schrijven
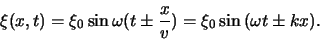 |
(40) |
Alternatief kunnen we schrijven
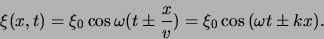 |
(41) |
Gebruikmakend van de stelling van Euler,
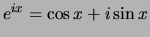 , kunnen
we een harmonische golf schrijven als superpositie van sin- en cos-functies
en vinden dan
, kunnen
we een harmonische golf schrijven als superpositie van sin- en cos-functies
en vinden dan
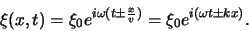 |
(42) |
Tenslotte merken we op dat een harmonische golf in drie dimensies geschreven
kan worden als
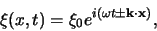 |
(43) |
waarbij
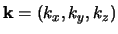 en
en
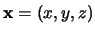 .
.




Next: Fourieranalyse van golfverschijnselen
Up: KLASSIEKE GOLFVERSCHIJNSELEN
Previous: Inleiding
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=10cm]{Figures/vervorming.eps}](img211.png)