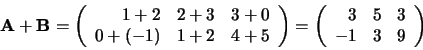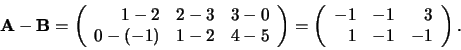Next: Product van scalar met
Up: Matrixrekening
Previous: Matrix als transformatie-operator
Contents
Als
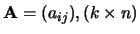 en
en
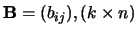 ,
dan is de afbeelding
,
dan is de afbeelding 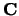 die aan
die aan
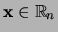 als
beeld toevoegt
als
beeld toevoegt
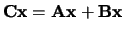 een lineaire
afbeelding. De transformatiematrix van deze afbeelding is
een lineaire
afbeelding. De transformatiematrix van deze afbeelding is
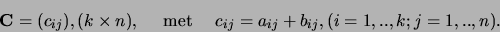 |
(233) |
Deze matrix 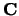 noemen we de som van matrices
noemen we de som van matrices  en
en 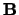 . Merk op dat enkel matrices van gelijke orde een som hebben.
De vermenigvuldiging met een kolomvector is distributief ten opzichte
van matrixoptelling. Bovendien is matrixoptelling commutatief en
associatief.
. Merk op dat enkel matrices van gelijke orde een som hebben.
De vermenigvuldiging met een kolomvector is distributief ten opzichte
van matrixoptelling. Bovendien is matrixoptelling commutatief en
associatief.
Voorbeeld: Als
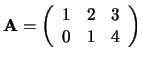 en
en
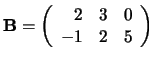 , dan
, dan
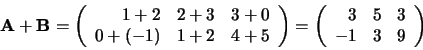 |
(234) |
en
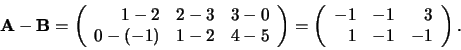 |
(235) |
Jo van den Brand
2004-09-25
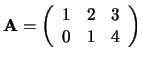 en
en
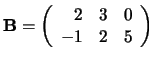 , dan
, dan