APPENDIX: COÖRDINATEN SYSTEMEN

CARTESIAANSE COÖRDINATEN

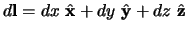$d{\bf l} = dx  \hat {\bf x} + dy  \hat {\bf y} + dz  \hat {\bf z}$ lijn-element

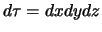$d\tau = dxdydz$ volume-element

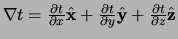$\nabla t = {\partial t \over \partial x} \hat {\bf x} + {\partial t \over \partial y} \hat {\bf y} + {\partial t \over \partial z} \hat {\bf z}$ gradiënt

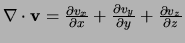$\nabla \cdot {\bf v} = {\partial v_x \over \partial x} + {\partial v_y \over \partial y} + {\partial v_z \over \partial z}$ divergentie

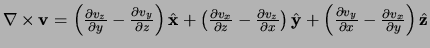$\nabla \times {\bf v} = \left( {\partial v_z \over \partial y} - {\partial v_... ...l v_y \over \partial x} - {\partial v_x \over \partial y} \right) \hat {\bf z}$ rotatie

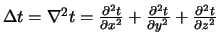$\Delta t = \nabla^2 t = {\partial^2 t \over \partial x^2} + {\partial^2 t \over \partial y^2} +{\partial^2 t \over \partial z^2}$ Laplace operator

SFERISCHE COÖRDINATEN

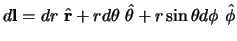$d{\bf l} = dr  \hat {\bf r} + r d\theta  \hat {\bf\theta} + r \sin {\theta}d\phi  \hat {\bf\phi}$ lijn-element

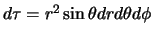$d\tau = r^2 \sin{\theta} dr d\theta d\phi$ volume-element

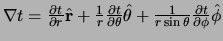$\nabla t = {\partial t \over \partial r} \hat {\bf r} + {1 \over r}{\partial t... ...eta} + {1 \over r \sin{\theta}}{\partial t \over \partial \phi} \hat {\bf\phi}$ gradiënt

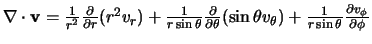$\nabla \cdot {\bf v} = {1 \over r^2}{\partial \over \partial r}(r^2 v_r) + {1 ... ...eta}v_\theta ) + {1 \over r \sin{\theta}}{\partial v_\phi \over \partial \phi}$ divergentie

$\nabla \times {\bf v} = {1 \over r \sin{\theta}} \left[ {\partial \over \parti... ...r} (r v_\theta ) - {\partial v_r \over \partial \theta }\right] \hat {\bf\phi}$ rotatie

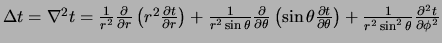$\Delta t = \nabla^2 t = {1 \over r^2}{\partial \over \partial r} \left( r^2 {\... ...a} \right) + {1 \over r^2 \sin^2{\theta} }{\partial^2 t \over \partial \phi^2}$ Laplace operator

CILINDRISCHE COÖRDINATEN

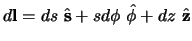$d{\bf l} = ds  \hat {\bf s} + s d\phi  \hat {\bf\phi} + dz  \hat {\bf z}$ lijn-element

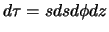$d\tau = sds d\phi dz$ volume-element

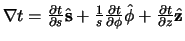$\nabla t = {\partial t \over \partial s} \hat {\bf s} + {1 \over s}{\partial t \over \partial \phi} \hat {\bf\phi} + {\partial t \over \partial z} \hat {\bf z}$ gradiënt

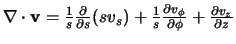$\nabla \cdot {\bf v} = {1 \over s}{\partial \over \partial s}(s v_s) + {1 \over s}{\partial v_\phi \over \partial \phi} + {\partial v_z \over \partial z}$ divergentie

$\nabla \times {\bf v} = \left[ {1 \over s}{\partial v_z \over \partial \phi} -... ...partial s}(sv_\phi ) - {\partial v_s \over \partial \phi} \right] \hat {\bf z}$ rotatie

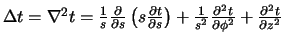$\Delta t = \nabla^2 t = {1 \over s}{\partial \over \partial s} \left( s {\part... ...r s^2}{\partial^2 t \over \partial \phi^2} + {\partial^2 t \over \partial z^2}$ Laplace operator

FUNDAMENTELE THEOREMAS

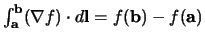$\int_{\bf a}^{\bf b} (\nabla f) \cdot d{\bf l} = f({\bf b}) - f({\bf a})$ Gradiënt theorema

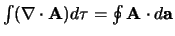$\int (\nabla \cdot {\bf A} ) d\tau = \oint {\bf A} \cdot d{\bf a}$ Divergentie theorema (stelling van Gauss)

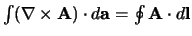$\int (\nabla \times {\bf A} ) \cdot d{\bf a} = \oint {\bf A} \cdot d{\bf l}$ Rotatie theorema (stelling van Stokes)