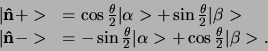Next: TIJDAFHANKELIJKE STORINGSREKENING
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Consequenties van een meting
Contents
Tenslotte beschouwen we de eigenwaarden en eigenfuncties van een
component van de spinoperator 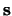 in de richting van een
eenheidsvector
in de richting van een
eenheidsvector 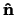 . Dit komt neer op het oplossen van de
eigenwaardenvergelijking
. Dit komt neer op het oplossen van de
eigenwaardenvergelijking
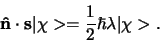 |
(591) |
Ter vereenvoudiging nemen we aan dat 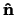 in het
in het
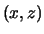 -vlak ligt en de componenten
-vlak ligt en de componenten
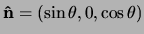 heeft, met
heeft, met
 en
en
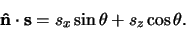 |
(592) |
Gebruik maken van de Pauli matrices levert
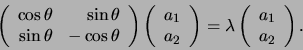 |
(593) |
Bovenstaande vergelijking kan eenvoudig worden opgelost. We
vinden de equivalente vergelijkingen
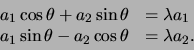 |
(594) |
Elk van deze vergelijkingen geeft een uitdrukking voor
de verhouding 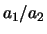 en het is eenvoudig na te gaan dat
de vergelijkingen enkel consistent zijn
als geldt dat
en het is eenvoudig na te gaan dat
de vergelijkingen enkel consistent zijn
als geldt dat
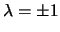 .
De eigenwaarden van
.
De eigenwaarden van
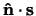 zijn dus
zijn dus
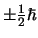 en hiermee zijn ze
hetzelfde19 als die van
en hiermee zijn ze
hetzelfde19 als die van 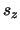 .
We vinden de relaties
.
We vinden de relaties
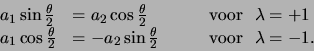 |
(595) |
De normalisatieconditie
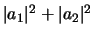 leidt
tot de genormeerde eigenvectoren
leidt
tot de genormeerde eigenvectoren
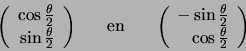 |
(596) |
voor 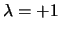 en
en 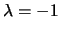 respectievelijk.
De willekeurige fasefactor in elk van deze eigenvectoren is
zodanig gekozen dat voor
respectievelijk.
De willekeurige fasefactor in elk van deze eigenvectoren is
zodanig gekozen dat voor 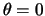 (corresponderend met
(corresponderend met
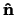 in de richting van de
in de richting van de 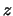 -as) de vectoren
samenvallen met de eigenvectoren
-as) de vectoren
samenvallen met de eigenvectoren 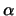 en
en 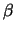 .
.
We duiden de eigenkets van
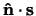 met
eigenwaarden
met
eigenwaarden
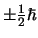 aan met
aan met
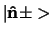 , dan vinden we
, dan vinden we
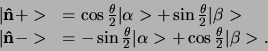 |
(597) |
Uit bovenstaande vergelijking kan men eenvoudig de waarschijnlijkheid
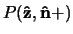 afleiden dat een meting van de
spincomponent
afleiden dat een meting van de
spincomponent
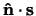 van een deeltje in de
toestand
van een deeltje in de
toestand 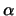 (dus met spin parallel aan de eenheidsvector
(dus met spin parallel aan de eenheidsvector
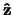 in de richting van de positieve
in de richting van de positieve 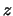 -as) het resultaat
-as) het resultaat
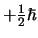 oplevert. Deze waarschijnlijkheid kan
verkregen worden door de expansie van
oplevert. Deze waarschijnlijkheid kan
verkregen worden door de expansie van
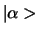 te beschouwen
in termen van de orthonormale spin eigentoestanden
te beschouwen
in termen van de orthonormale spin eigentoestanden
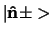 en wordt gegeven
door
en wordt gegeven
door
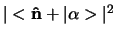 . We vinden
. We vinden
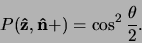 |
(598) |
Dit belangrijke resultaat zullen we nodig hebben tijdens de discussie van
de ongelijkheid van Bell.




Next: TIJDAFHANKELIJKE STORINGSREKENING
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Consequenties van een meting
Contents
Jo van den Brand
2004-09-25
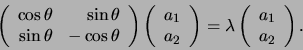
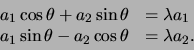
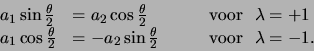
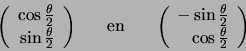
![]() met
eigenwaarden
met
eigenwaarden
![]() aan met
aan met
![]() , dan vinden we
, dan vinden we