1989 Results (Gepner models)

These are scanned pdf files of the Gepner model simple current Hodge scan made in 1989 in collaboration with Shimon Yankielowicz.

The scan covers all simple current invariants that can be obtained by multiplying the modular matrices of simple current MIPFs defined by a single current. These currents were selected at random. Up to eight

single current matrices are multiplied.

All spectra have at least N=1 supersymmetry and E6 or SO(10) gauge symmetry.

File 1

File 2

File 3

File 4

File 5

File 6

The following paper contains a summary of the result, with spectra organized according to their Hodge numbers (and other data). These tables only contain the (2,2) spectra.

Summary

2008 Results (Gepner models)

These are files from a scan done in 2008. Unlike the 1989 results these are not based on random selection, but on a complete enumeration of all the MIPFs.

Gepner Hodge number files

There are 168 files of type “.hodge_summary”, one for each Gepner model combination.

Each file contains lines of the form

  nr.   5 [found as nr.   3]:          10 x   (40,4,252,8,8,4,4,1)

These numbers are respectively a sequential label, a label indicating the original order in which these MIPFs were found, and the multiplicity. Typically, the multiplicity is 1, in other words every MIPF generates a distinct spectrum. If low-level factors (in particular k=1 and k=2) occur in the tensor product there may be degeneracies.

The numbers between parentheses are respectively the hodge numbers h11, h12, the number of singlets occurring in a heterotic spectrum, the number of additional (i.e. in addition to E6 vector bosons in a heterotic spectrum in the left or right algebra (if the left resp. the right algebra is used as a bosonic sector in a heterotic string), the number of left- and right supersymmetries, and an integer indicating if the MIPF is symmetric (1) or not (0).

In a few cases (namely (1,1,1,1,1,1,1,1,1), (1,1,1,1,1,1,4) and (1,1,1,1,1,4,4)) the total number of asymmetric MIPFs was too large to enumerate, and in this case a randomized scan was done, allowing only a limited number of “discrete torsion” values for each simple current group. In all cases those scans were extensive enough to ensure that most likely nothing was missed.

Complete scans will always display exact mirror symmetry.

Additional files in the downloaded directory are explained below, under “Summary”.

2008 Results (Free Fermion Models)

These are files from a scan done in 2008, in collaboration with M. Lennek and E. Kiritsis.

Most of these runs were done by M. Lennek.

Free Fermion Hodge number files

There are 62 files, one for each realization of world-sheet supersymmetry. The format is as above, except that only symmetric MIPFs are considered here, and the last number indicating

(a)symmetry is therefore not listed. Included in this directory are the original kac input files, defining the word-sheet supersymmetry projection.

Summary

We can distinguish all the aforementioned spectra on the basis of several criteria:

1. Euler numbers 2 x (h11-h12)
   

2. Hodge pairs h11, h12
   

3. Hodge triplets h11, h12, singlets
   

4. Hodge quartets h11, h12, singlets and extra (in addition to E6) vector bosons
   

In addition, it is useful to consider “Higgsed triplets”, where h11, h12 and the difference between singlets and vector bosons are considered. The idea is that some spectra differ only because a vector bosons has absorbed a singlet to acquire mass.

The total number for each of these kinds of spectra are as follows:

Symmetric Gepner model MIPFs:

1. Distinct Euler numbers: 113
   

2. Distinct Hodge Pairs: 868
   

3. Distinct Hodge Triplets: 1767
   

4. Distinct Spectra (Quartets): 1785
   

5. Distinct Spectra (Higgsed): 1681
   

Symmetric plus asymmetric Gepner model MIPFs:

1. Distinct Euler numbers: 115
   

2. Distinct Hodge Pairs: 906
   

3. Distinct Hodge Triplets: 1981
   

4. Distinct Spectra (Quartets): 2013
   

5. Distinct Spectra (Higgsed): 1885
   

Free Fermionic MIPFs:

1. Distinct Euler numbers: 9
   

2. Distinct Hodge Pairs: 26
   

3. Distinct Hodge Triplets: 363
   

4. Distinct Spectra (Quartets): 382
   

5. Distinct Spectra (Higgsed): 284
   

Symmetric, asymmetric Gepner MIPFs combined with free fermions:

1. Distinct Euler numbers: 115
   

2. Distinct Hodge Pairs: 906
   

3. Distinct Hodge Triplets: 2306
   

4. Distinct Spectra (Quartets): 2373
   

5. Distinct Spectra (Higgsed): 2134
   

Note that

1. -Distinct spectra are almost completely distinguished by triplets
   

2. -There is some evidence for a Higgs relationship between some spectra
   

3. -Free fermions add nothing to the list of Hodge pairs
   

The additional files in the Gepner model directory are

1. -All_Gepner_symmetric
   

2. -All_Gepner_asymmetric
   

3. -All_Fermionic
   

These file contain the raw data from all hodge_summary files, with identical lines removed, and order according to |h11-h12| (the first entry on each line).

Furthermore there are files Euler, Hodge, Quartets, Triplets containing the lists of the first four spectrum types explained above for all Gepner models. The first entry in the latter three files is h11-h12, by which all entries are ordered. For each of these four files there is also one with “_symmetric” and “_total” attached to their names. They contain the same information for symmetric Gepner MIPFs only, and for the total, all Gepner MIPFs and fermionic MIPFs combined.

Comparison with Calabi-Yau and Landau-Ginzburg data

The CY and LG data are from the home page of Max Kreuzer.

There are 30108 hodge pairs from “reflexive polyhedra”. The set of 4370 LG Hodge

pairs we consider is a combination of the three classes listed, namely “untwisted models”,

“abelian orbifolds” and “discrete torsion”.

So we consider four classes, denoted as CY, LG, Gepner, Free Fermion.

Total number of CY hodge pairs: 30108

Total number of LG hodge pairs: 4370

Total number of Gepner hodge pairs: 906

Total number of Free Fermion hodge pairs: 26

The overlaps between these sets are as follows

Free Fermion overlap

All contained in Hodge

Not contained in CY: 16

All contained in LG

Hodge overlap

Not contained in Free Fermion: 880

Not contained in CY: 112

All contained in LG

LG overlap

Not contained in Free Fermion: 4344

Not contained in CY: 200

Not contained in Hodge: 3464

CY overlap

Not contained in Free Fermion: 30098

Not contained in LG: 25938

Not contained in Hodge: 29314

This means that the Free fermion class is fully contained in the Gepner class,

which in its turn is fully contained in the LG class. However, the LG class is not fully contained in the CY class.

This is graphical comparison between the classes. On the horizontal axis is the number of families, the absolute value of h11-h12. On the vertical axis we put the total number of distinct Hodge pairs for a given number of families.

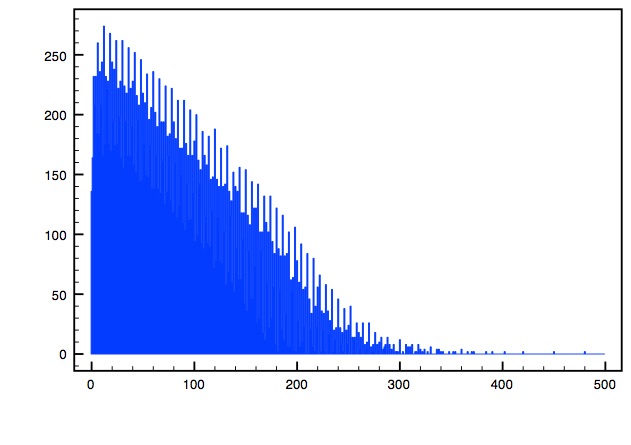
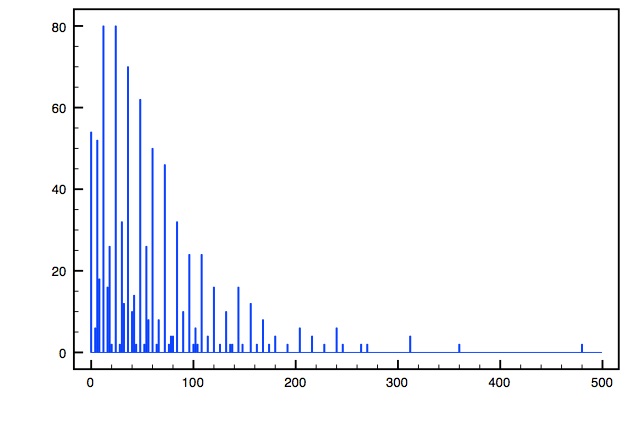
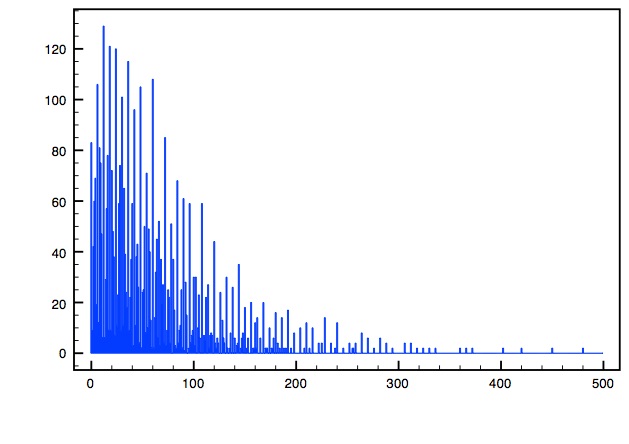
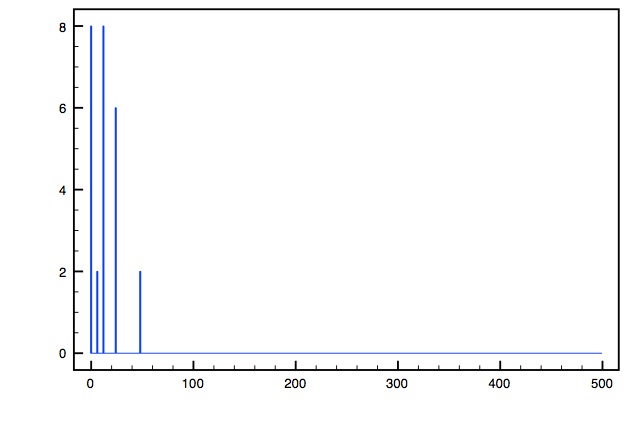
Free Fermion

Gepner

LG

CY