



Next: Matrixrekening
Up: Lineaire ruimten en lineaire
Previous: Inwendig product, norm en
Contents
Een afbeelding van de verzameling 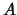 naar de verzameling
naar de verzameling 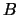 is
een relatie waarvan
is
een relatie waarvan 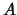 de originelenverzameling is en
de originelenverzameling is en 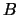 de
beeldverzameling omvat, terwijl elk origineel één beeld heeft
(een functie is dus een afbeelding).
de
beeldverzameling omvat, terwijl elk origineel één beeld heeft
(een functie is dus een afbeelding).
Definitie: Een afbeelding 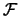 van de lineaire ruimte
van de lineaire ruimte
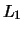 naar de lineaire ruimte
naar de lineaire ruimte 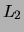 heet een lineaire afbeelding
als
heet een lineaire afbeelding
als
-
![$\forall_{{\bf a},{\bf b} \in L_1}
[ {\mathcal{F}} ({\bf a} + {\bf b})
= {\mathcal{F}}({\bf a}) + {\mathcal{F}} ({\bf b}) ]$](img752.png) en
en
-
![$\forall_{{\bf a} \in L_1, p \in {\mathbb{R}}}
[ {\mathcal{F}} (p{\bf a}) = p {\mathcal{F}}({\bf a}) ]$](img753.png) .
.
Merk op dat als
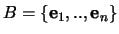 een basis is van
een basis is van 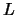 dan is de afbeelding van
dan is de afbeelding van 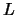 naar
naar
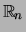 , waarvoor geldt dat
het beeld van
, waarvoor geldt dat
het beeld van
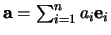 de `kentalvector'
de `kentalvector'
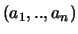 is, een lineaire afbeelding.
is, een lineaire afbeelding.
Jo van den Brand
2004-09-25
![]() van de lineaire ruimte
van de lineaire ruimte
![]() naar de lineaire ruimte
naar de lineaire ruimte ![]() heet een lineaire afbeelding
als
heet een lineaire afbeelding
als