



Next: Inwendig product, norm en
Up: Lineaire ruimten en lineaire
Previous: Eigenschappen
Contents
Definitie: Een deelverzameling 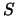 van een lineaire ruimte
van een lineaire ruimte 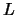 heet een onafhankelijke stelsel vectoren als
heet een onafhankelijke stelsel vectoren als
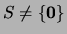 ,
terwijl geen enkel element van
,
terwijl geen enkel element van 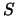 gelijk is aan een lineaire combinatie
van andere elementen van
gelijk is aan een lineaire combinatie
van andere elementen van 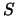 .
.
Stelling 1: Als 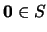 , dan is
, dan is 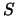 een afhankelijk
stelsel.
een afhankelijk
stelsel.
Stelling 2:
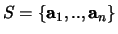 is dan en
slechts dan een onafhankelijk stelsel als uit
is dan en
slechts dan een onafhankelijk stelsel als uit
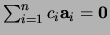 volgt dat
volgt dat 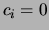 voor
alle
voor
alle 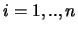 .
.
Definitie: 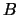 heet een basis van de lineaire ruimte
heet een basis van de lineaire ruimte 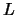 als
als
-
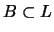 ,
,
-
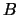 een onafhankelijk stelsel is,
een onafhankelijk stelsel is,
- elk element van
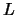 gelijk is aan een lineaire combinatie van
elementen van
gelijk is aan een lineaire combinatie van
elementen van 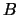 .
.
Als
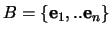 dan geldt
dan geldt
![\begin{displaymath}
\forall_{{\bf a} \in L} \exists_{{\bf a}_1, .., {\bf a}_n \...
...b{R}}}
\left[ {\bf a} = \sum_{i=1}^n a_i {\bf e}_i \right] .
\end{displaymath}](img727.png) |
(223) |
Deze getallen 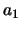 tot en met
tot en met 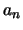 heten de kentallen van
heten de kentallen van 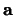 ten opzichte van de basis
ten opzichte van de basis 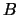 . We noemen
. We noemen
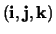 `de' basis van
`de' basis van 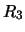 van de drietallige getalgrepen.
van de drietallige getalgrepen.
Stelling 3: Als de lineaire ruimte 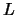 een basis heeft die uit
een basis heeft die uit
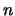 elementen bestaat, dan bestaat elke basis van
elementen bestaat, dan bestaat elke basis van 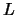 uit
uit 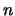 elementen.
elementen.
Definitie: De dimensie van 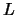 is het aantal elementen
van de basis van
is het aantal elementen
van de basis van 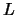 .
.




Next: Inwendig product, norm en
Up: Lineaire ruimten en lineaire
Previous: Eigenschappen
Contents
Jo van den Brand
2004-09-25
![]() , dan is
, dan is ![]() een afhankelijk
stelsel.
een afhankelijk
stelsel.
![]() is dan en
slechts dan een onafhankelijk stelsel als uit
is dan en
slechts dan een onafhankelijk stelsel als uit
![]() volgt dat
volgt dat ![]() voor
alle
voor
alle ![]() .
.
![]() heet een basis van de lineaire ruimte
heet een basis van de lineaire ruimte ![]() als
als
![\begin{displaymath}
\forall_{{\bf a} \in L} \exists_{{\bf a}_1, .., {\bf a}_n \...
...b{R}}}
\left[ {\bf a} = \sum_{i=1}^n a_i {\bf e}_i \right] .
\end{displaymath}](img727.png)
![]() een basis heeft die uit
een basis heeft die uit
![]() elementen bestaat, dan bestaat elke basis van
elementen bestaat, dan bestaat elke basis van ![]() uit
uit ![]() elementen.
elementen.
![]() is het aantal elementen
van de basis van
is het aantal elementen
van de basis van ![]() .
.