



Next: Eigenschappen
Up: Lineaire ruimten en lineaire
Previous: Lineaire ruimten en lineaire
Contents
Elke verzameling, waarbinnen de elementen `opgeteld' en `met een
scalar vermenigvuldigd' kunnen worden,
wordt een lineaire ruimte ofwel een vectorruimte
genoemd en de elementen ervan heten vectoren.
Definitie: Een verzameling 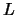 heet een lineaire ruimte
over een getallenlichaam
heet een lineaire ruimte
over een getallenlichaam 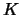 als geldt
als geldt
-
![$\forall_{{\bf a},{\bf a} \in L} \exists !_{{\bf c} \in L}
[ {\bf a} + {\bf b} = {\bf c} ]$](img699.png)
-
![$\forall_{p \in K,{\bf a} \in L } \exists !_{b \in L}
[ p{\bf a} = {\bf b} ]$](img700.png) ,
,
terwijl de volgende acht axioma's gelden
-
![$\forall_{{\bf a},{\bf b} \in L} [ {\bf a} + {\bf b} = {\bf b} + {\bf a} ]$](img701.png)
-
![$\forall_{{\bf a},{\bf b},{\bf c} \in L}
[ ({\bf a} + {\bf b}) + {\bf c}= {\bf a} + ({\bf b} + {\bf c}) ]$](img702.png)
-
![$\exists_{{\bf0} \in L} \forall_{{\bf a} \in L}
[ {\bf a} + {\bf0} = {\bf a} ]$](img703.png)
-
![$\forall_{{\bf a} \in L} \exists_{{- \bf a} \in L}
[ {\bf a} + (-{\bf a}) = {\bf0} ]$](img704.png)
-
![$\forall_{p,q \in K, {\bf a} \in L}
[ (p+q){\bf a} = p{\bf a} + q{\bf a} ]$](img705.png)
-
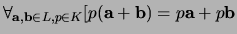
-
![$\forall_{p,q \in K, {\bf a} \in L}
[ p(q{\bf a}) = (pq){\bf a} ]$](img707.png)
-
![$\forall_{{\bf a} \in L} [ 1{\bf a} = {\bf a} ]$](img708.png)
We hebben in hoofdstuk 1.1 reeds gezien dat
vectoren aan bovenstaande axioma's voldoen. Hier bekijken
we een en ander op meer abstractie wijze en
het getallenlichaam 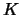 kan
kan
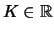 , respectievelijk
, respectievelijk
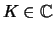 , zijn. Men spreekt dan van een reële,
respectievelijk complexe, vectorruimte
, zijn. Men spreekt dan van een reële,
respectievelijk complexe, vectorruimte 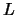 . In paragraaf 1.1
hebben we ons beperkt tot een discussie van reële vectorruimten.
Ook in deze paragraaf beschouwen we enkel reële vectorruimten.
Later zullen we de discussie uitbreiden tot complexe vectorruimten.
. In paragraaf 1.1
hebben we ons beperkt tot een discussie van reële vectorruimten.
Ook in deze paragraaf beschouwen we enkel reële vectorruimten.
Later zullen we de discussie uitbreiden tot complexe vectorruimten.
Jo van den Brand
2004-09-25
![]() heet een lineaire ruimte
over een getallenlichaam
heet een lineaire ruimte
over een getallenlichaam ![]() als geldt
als geldt