Opdracht 7
a) Niet waar, het inprodukt van twee vektoren is een getal.
b) Omdat |![[Graphics:Images/e+m2_gr_1.gif]](Images/e+m2_gr_1.gif) | = 1 geldt:
| = 1 geldt:
![[Graphics:Images/e+m2_gr_2.gif]](Images/e+m2_gr_2.gif) = |
= |![[Graphics:Images/e+m2_gr_3.gif]](Images/e+m2_gr_3.gif) | |
| |![[Graphics:Images/e+m2_gr_4.gif]](Images/e+m2_gr_4.gif) | cos(
| cos(![[Graphics:Images/e+m2_gr_5.gif]](Images/e+m2_gr_5.gif) ) = |
) = |![[Graphics:Images/e+m2_gr_6.gif]](Images/e+m2_gr_6.gif) | cos(
| cos(![[Graphics:Images/e+m2_gr_7.gif]](Images/e+m2_gr_7.gif) ).
).
Dit is de component van ![[Graphics:Images/e+m2_gr_8.gif]](Images/e+m2_gr_8.gif) in de richting van
in de richting van ![[Graphics:Images/e+m2_gr_9.gif]](Images/e+m2_gr_9.gif) .
.
c) Met d![[Graphics:Images/e+m2_gr_10.gif]](Images/e+m2_gr_10.gif) wordt bedoeld
wordt bedoeld ![[Graphics:Images/e+m2_gr_11.gif]](Images/e+m2_gr_11.gif) dO. Als je nu invult
dO. Als je nu invult ![[Graphics:Images/e+m2_gr_12.gif]](Images/e+m2_gr_12.gif) =
= ![[Graphics:Images/e+m2_gr_13.gif]](Images/e+m2_gr_13.gif) krijg je:
krijg je:
![[Graphics:Images/e+m2_gr_14.gif]](Images/e+m2_gr_14.gif) =
= ![[Graphics:Images/e+m2_gr_15.gif]](Images/e+m2_gr_15.gif) O =
O = ![[Graphics:Images/e+m2_gr_16.gif]](Images/e+m2_gr_16.gif) = O.
= O.
Opdracht 8
a) Totale lading: Q = ![[Graphics:Images/e+m2_gr_17.gif]](Images/e+m2_gr_17.gif) = ρ
= ρ ![[Graphics:Images/e+m2_gr_18.gif]](Images/e+m2_gr_18.gif) = ρ
= ρ ![[Graphics:Images/e+m2_gr_19.gif]](Images/e+m2_gr_19.gif) π
π ![[Graphics:Images/e+m2_gr_20.gif]](Images/e+m2_gr_20.gif) .
.
b) Het gemiddelde van ρ (r) is ![[Graphics:Images/e+m2_gr_21.gif]](Images/e+m2_gr_21.gif)
![[Graphics:Images/e+m2_gr_22.gif]](Images/e+m2_gr_22.gif) , dus je zou misschien denken dat de totale lading
, dus je zou misschien denken dat de totale lading
twee keer zo klein is.
c) ρ (r) = a*r + b, met ρ (0) = ![[Graphics:Images/e+m2_gr_23.gif]](Images/e+m2_gr_23.gif) en ρ (R) = 0. Oplossen levert: b =
en ρ (R) = 0. Oplossen levert: b = ![[Graphics:Images/e+m2_gr_24.gif]](Images/e+m2_gr_24.gif) en a = -
en a = -![[Graphics:Images/e+m2_gr_25.gif]](Images/e+m2_gr_25.gif) .
.
d) Q = ![[Graphics:Images/e+m2_gr_26.gif]](Images/e+m2_gr_26.gif) =
= ![[Graphics:Images/e+m2_gr_27.gif]](Images/e+m2_gr_27.gif) -
- ![[Graphics:Images/e+m2_gr_28.gif]](Images/e+m2_gr_28.gif) =
= ![[Graphics:Images/e+m2_gr_29.gif]](Images/e+m2_gr_29.gif)
![[Graphics:Images/e+m2_gr_30.gif]](Images/e+m2_gr_30.gif) π
π ![[Graphics:Images/e+m2_gr_31.gif]](Images/e+m2_gr_31.gif) -
- ![[Graphics:Images/e+m2_gr_32.gif]](Images/e+m2_gr_32.gif)
![[Graphics:Images/e+m2_gr_33.gif]](Images/e+m2_gr_33.gif)
![[Graphics:Images/e+m2_gr_34.gif]](Images/e+m2_gr_34.gif)
![[Graphics:Images/e+m2_gr_35.gif]](Images/e+m2_gr_35.gif)
![[Graphics:Images/e+m2_gr_36.gif]](Images/e+m2_gr_36.gif) sin θ dr dθ dϕ .
sin θ dr dθ dϕ .
De integralen over θ en ϕ leveren een factor 4π, de integraal over r wordt ![[Graphics:Images/e+m2_gr_37.gif]](Images/e+m2_gr_37.gif) =
= ![[Graphics:Images/e+m2_gr_38.gif]](Images/e+m2_gr_38.gif)
![[Graphics:Images/e+m2_gr_39.gif]](Images/e+m2_gr_39.gif) . Uiteindelijk krijgen we dan:
. Uiteindelijk krijgen we dan:
Q = ![[Graphics:Images/e+m2_gr_40.gif]](Images/e+m2_gr_40.gif)
![[Graphics:Images/e+m2_gr_41.gif]](Images/e+m2_gr_41.gif) π
π ![[Graphics:Images/e+m2_gr_42.gif]](Images/e+m2_gr_42.gif) -
- ![[Graphics:Images/e+m2_gr_43.gif]](Images/e+m2_gr_43.gif) π
π ![[Graphics:Images/e+m2_gr_44.gif]](Images/e+m2_gr_44.gif) =
= ![[Graphics:Images/e+m2_gr_45.gif]](Images/e+m2_gr_45.gif)
![[Graphics:Images/e+m2_gr_46.gif]](Images/e+m2_gr_46.gif) π
π ![[Graphics:Images/e+m2_gr_47.gif]](Images/e+m2_gr_47.gif) .
.
e) De totale lading is dus vier keer zo klein geworden, en niet twee keer. Dit kun je verklaren door te bedenken dat de inhoud van een bolschilletje met dikte dr, 4π![[Graphics:Images/e+m2_gr_48.gif]](Images/e+m2_gr_48.gif) dr is. Hoe groter r, des te groter dus deze inhoud, en des te groter ook de bijdrage aan de integraal. Dit zorgt ervoor dat de integraal meer dan twee keer zo klein wordt, immers ρ(r) is klein voor grote r.
dr is. Hoe groter r, des te groter dus deze inhoud, en des te groter ook de bijdrage aan de integraal. Dit zorgt ervoor dat de integraal meer dan twee keer zo klein wordt, immers ρ(r) is klein voor grote r.
Opdracht 9
a)
![[Graphics:Images/e+m2_gr_49.gif]](Images/e+m2_gr_49.gif)
b) Voor de flux geldt: φ = ![[Graphics:Images/e+m2_gr_50.gif]](Images/e+m2_gr_50.gif) . In de figuur zien we dat
. In de figuur zien we dat ![[Graphics:Images/e+m2_gr_51.gif]](Images/e+m2_gr_51.gif) altijd loodrecht op het oppervlak staat, dus
altijd loodrecht op het oppervlak staat, dus ![[Graphics:Images/e+m2_gr_52.gif]](Images/e+m2_gr_52.gif) = |
= |![[Graphics:Images/e+m2_gr_53.gif]](Images/e+m2_gr_53.gif) |. Verder is de afstand tot de oorsprong constant op het oppervlak, en dus is de grootte van
|. Verder is de afstand tot de oorsprong constant op het oppervlak, en dus is de grootte van ![[Graphics:Images/e+m2_gr_54.gif]](Images/e+m2_gr_54.gif) ook constant want die hangt alleen van |
ook constant want die hangt alleen van |![[Graphics:Images/e+m2_gr_55.gif]](Images/e+m2_gr_55.gif) | af. We krijgen dus:
| af. We krijgen dus:
φ = E ![[Graphics:Images/e+m2_gr_56.gif]](Images/e+m2_gr_56.gif) =
= ![[Graphics:Images/e+m2_gr_57.gif]](Images/e+m2_gr_57.gif)
![[Graphics:Images/e+m2_gr_58.gif]](Images/e+m2_gr_58.gif) sin
sin ![[Graphics:Images/e+m2_gr_59.gif]](Images/e+m2_gr_59.gif)
![[Graphics:Images/e+m2_gr_60.gif]](Images/e+m2_gr_60.gif)
c) Als er 'iets' is wat door een oppervlak gaat, kun je spreken van flux. Bij licht gaat het om fotonen, bij geluid om geluidsgolven, en bij een radioactieve bron om radioactieve deeltjes.
d) Er geldt: 0,01*h=0,01*![[Graphics:Images/e+m2_gr_61.gif]](Images/e+m2_gr_61.gif) +
+ ![[Graphics:Images/e+m2_gr_62.gif]](Images/e+m2_gr_62.gif) t +
t + ![[Graphics:Images/e+m2_gr_63.gif]](Images/e+m2_gr_63.gif) a
a ![[Graphics:Images/e+m2_gr_64.gif]](Images/e+m2_gr_64.gif) (h is in centimeters, vandaar de factoren 0,01). We weten:
(h is in centimeters, vandaar de factoren 0,01). We weten: ![[Graphics:Images/e+m2_gr_65.gif]](Images/e+m2_gr_65.gif) = 0 m,
= 0 m, ![[Graphics:Images/e+m2_gr_66.gif]](Images/e+m2_gr_66.gif) = 0,1 m/s, en a = 9,8 m/
= 0,1 m/s, en a = 9,8 m/![[Graphics:Images/e+m2_gr_67.gif]](Images/e+m2_gr_67.gif) . Als we hieruit t oplossen krijgen we:
. Als we hieruit t oplossen krijgen we:
t=![[Graphics:Images/e+m2_gr_68.gif]](Images/e+m2_gr_68.gif) . (we willen dat t>0 , dus de negatieve oplossing doet niet mee)
. (we willen dat t>0 , dus de negatieve oplossing doet niet mee)
Verder weten we v = ![[Graphics:Images/e+m2_gr_69.gif]](Images/e+m2_gr_69.gif) + a*t = 0,1 + 9,8 t . Vullen we t in dan vinden we: v =
+ a*t = 0,1 + 9,8 t . Vullen we t in dan vinden we: v = ![[Graphics:Images/e+m2_gr_70.gif]](Images/e+m2_gr_70.gif) .
.
e) Als de fluxen elkaar niet opheffen dan neemt de hoeveelheid water in de straal toe of af. Dit kan natuurlijk niet eeuwig doorgaan; na verloop van tijd moet de hoeveelheid water constant blijven, oftewel de fluxen zijn gelijk.
f) De flux is hier de hoeveelheid water die per seconde door het oppervlak stroomt. Dit is gelijk aan A*v, oppervlakte keer snelheid (merk op, dit heeft de dimensie ![[Graphics:Images/e+m2_gr_71.gif]](Images/e+m2_gr_71.gif) / s, inderdaad dus een hoeveelheid per seconde). De diameter van de straal bij h=0 is 1 cm. De flux aldaar moet gelijk zijn aan de flux op een hoogte h. We krijgen dan:
/ s, inderdaad dus een hoeveelheid per seconde). De diameter van de straal bij h=0 is 1 cm. De flux aldaar moet gelijk zijn aan de flux op een hoogte h. We krijgen dan:
π * ![[Graphics:Images/e+m2_gr_72.gif]](Images/e+m2_gr_72.gif) * 0,1 = π *
* 0,1 = π * ![[Graphics:Images/e+m2_gr_73.gif]](Images/e+m2_gr_73.gif) *
* ![[Graphics:Images/e+m2_gr_74.gif]](Images/e+m2_gr_74.gif) .
.
Als we hieruit d oplossen krijgen we
d = ![[Graphics:Images/e+m2_gr_75.gif]](Images/e+m2_gr_75.gif)
Opdracht 10
a) Om de wet van Gauss toe te passen moet je de oppervlakte-integraal ![[Graphics:Images/e+m2_gr_76.gif]](Images/e+m2_gr_76.gif) uitrekenen, met A een gesloten oppervlak waar het geladen voorwerp zich in bevindt. Deze integraal is alleen makkelijk uit te rekenen als er een symmetrie in het systeem zit. De drie symmetrieen die 'werken' zijn: sferische symmetrie, vlaksymmetrie, en cylindrische symmetrie. Zie ook bijv. Griffiths p. 71. Een geladen bal (lading Q) is sferisch symmetrisch, dit gaat dus werken. Kies voor A een bolschil om de bal heen, dan is
uitrekenen, met A een gesloten oppervlak waar het geladen voorwerp zich in bevindt. Deze integraal is alleen makkelijk uit te rekenen als er een symmetrie in het systeem zit. De drie symmetrieen die 'werken' zijn: sferische symmetrie, vlaksymmetrie, en cylindrische symmetrie. Zie ook bijv. Griffiths p. 71. Een geladen bal (lading Q) is sferisch symmetrisch, dit gaat dus werken. Kies voor A een bolschil om de bal heen, dan is ![[Graphics:Images/e+m2_gr_77.gif]](Images/e+m2_gr_77.gif) overal op de bolschil constant en kunnen we dat dus buiten de integraal halen. Uit de stelling van Gauss volgt dan:
overal op de bolschil constant en kunnen we dat dus buiten de integraal halen. Uit de stelling van Gauss volgt dan:
![[Graphics:Images/e+m2_gr_78.gif]](Images/e+m2_gr_78.gif) =
= ![[Graphics:Images/e+m2_gr_79.gif]](Images/e+m2_gr_79.gif) = E
= E ![[Graphics:Images/e+m2_gr_80.gif]](Images/e+m2_gr_80.gif) = E 4 π
= E 4 π ![[Graphics:Images/e+m2_gr_81.gif]](Images/e+m2_gr_81.gif) ,
,
E = ![[Graphics:Images/e+m2_gr_82.gif]](Images/e+m2_gr_82.gif) .
.
b) Een schoen is zeker niet symmetrisch, we hebben dus weinig aan de stelling van Gauss.
c) Van een oneindig grote plaat kun je eenvoudig met de stelling van Gauss het veld berekenen (het systeem heeft vlaksymmetrie). Zie p. 49 van de transparanten. Je vindt: E = ![[Graphics:Images/e+m2_gr_83.gif]](Images/e+m2_gr_83.gif) .
.
Het veld van een dozijn platen kun je dan vinden door de bijdrage van elke plaat afzonderlijk op te tellen (superpositiebeginsel).
d) Een kubus heeft niet een van de drie symmetrieen bij a). Gauss helpt dus hier niet.
Opdracht 12
a) ![[Graphics:Images/e+m2_gr_84.gif]](Images/e+m2_gr_84.gif) =
= ![[Graphics:Images/e+m2_gr_85.gif]](Images/e+m2_gr_85.gif) (
( ![[Graphics:Images/e+m2_gr_86.gif]](Images/e+m2_gr_86.gif) +
+ ![[Graphics:Images/e+m2_gr_87.gif]](Images/e+m2_gr_87.gif) ), en evenzo voor de andere ladingen (de krachten op B zijn natuurlijk wel tegengesteld).
), en evenzo voor de andere ladingen (de krachten op B zijn natuurlijk wel tegengesteld).
b) Het veld op x = 1 cm: E = | - ![[Graphics:Images/e+m2_gr_88.gif]](Images/e+m2_gr_88.gif) +
+ ![[Graphics:Images/e+m2_gr_89.gif]](Images/e+m2_gr_89.gif) -
- ![[Graphics:Images/e+m2_gr_90.gif]](Images/e+m2_gr_90.gif) | = 5,4
| = 5,4 ![[Graphics:Images/e+m2_gr_91.gif]](Images/e+m2_gr_91.gif) N / C. Evenzo vinden we 3,37
N / C. Evenzo vinden we 3,37 ![[Graphics:Images/e+m2_gr_92.gif]](Images/e+m2_gr_92.gif) N / C op x = 2 cm, en
N / C op x = 2 cm, en
6,66 ![[Graphics:Images/e+m2_gr_93.gif]](Images/e+m2_gr_93.gif) N / C op x = 3 cm. De waarde bij x = 2 cm is 16 =
N / C op x = 3 cm. De waarde bij x = 2 cm is 16 = ![[Graphics:Images/e+m2_gr_94.gif]](Images/e+m2_gr_94.gif) keer zo klein als die voor x = 1 cm, terwijl x 2 keer zo groot is. En de waarde bij x = 3 cm is 81 =
keer zo klein als die voor x = 1 cm, terwijl x 2 keer zo groot is. En de waarde bij x = 3 cm is 81 = ![[Graphics:Images/e+m2_gr_95.gif]](Images/e+m2_gr_95.gif) keer zo klein als die voor x = 1 cm. Het veld neemt dus af met
keer zo klein als die voor x = 1 cm. Het veld neemt dus af met ![[Graphics:Images/e+m2_gr_96.gif]](Images/e+m2_gr_96.gif) .
.
c) Omdat in een watermolecuul een knik zit, is er een positieve kant (waar de waterstofatomen zitten) en een negatieve kant (waar het zuurstofatoom zit). Dit is dus een dipool, het veld valt af met de derde macht. Koolstofdioxide lijkt meer op de configuratie van vraag B, het molecuul is recht. Het veld zal afvallen met de vierde macht.
Opdracht 13
a) Nee dat kan niet. Mocht je denken dat je vanwege de wet van Gauss alleen te maken hebt met de lading die dichter bij de oorsprong ligt dan het punt waarin je kijkt, dan vergeet je dat de wet van Gauss alleen iets zegt over de bijdrage van een lading aan de oppervlakte-integraal van de normale component van het elektrisch veld. Dat de bijdrage van een lading aan de integraal nul is, wil niet zeggen dat de bijdrage in elk punt nul is.
b) Een puntlading is een standaardgeval: E = ![[Graphics:Images/e+m2_gr_97.gif]](Images/e+m2_gr_97.gif) .
.
c) Het veld is in ieder geval naar buiten gericht en in grootte alleen afhankelijk van de afstand tot het middelpunt. De oppervlakte-integraal die in de wet van Gauss vookomt is dus gelijk aan EO. Zolang het boloppervlak O binnen de bolschil ligt, is er geen omsloten lading. EO is dan nul, en omdat O geen nul is, is E nul (dit kan alleen omdat je weet dat het veld radieel is, alleen daardoor weet je dat de integraal EO is). Buiten de bolschil is de omsloten lading gelijk aan de totale lading. Het verloop is verder net zo als wanneer alle lading in het middelpunt van de bolschil had gezeten.
d) Neem een boloppervlak O met straal r (<R ). Om de ingesloten lading te bepalen moeten we ρ integreren tot aan r: ![[Graphics:Images/e+m2_gr_98.gif]](Images/e+m2_gr_98.gif) = 4 π
= 4 π ![[Graphics:Images/e+m2_gr_99.gif]](Images/e+m2_gr_99.gif) = Q
= Q ![[Graphics:Images/e+m2_gr_100.gif]](Images/e+m2_gr_100.gif) . We weten weer dat E loodrecht op het oppervlak staat en alleen van |r| afhangt, dus
. We weten weer dat E loodrecht op het oppervlak staat en alleen van |r| afhangt, dus ![[Graphics:Images/e+m2_gr_101.gif]](Images/e+m2_gr_101.gif) = E 4 π
= E 4 π ![[Graphics:Images/e+m2_gr_102.gif]](Images/e+m2_gr_102.gif) . We vinden dus: E =
. We vinden dus: E = ![[Graphics:Images/e+m2_gr_103.gif]](Images/e+m2_gr_103.gif) Q
Q ![[Graphics:Images/e+m2_gr_104.gif]](Images/e+m2_gr_104.gif) =
= ![[Graphics:Images/e+m2_gr_105.gif]](Images/e+m2_gr_105.gif) .
.
Buiten de bol is het veld weer net zoals dat van een puntlading Q.
e) Dit is duidelijk weer een radieel probleem. De integraal komt weer neer op EO, de waarde maal de oppervlakte.
Tot R1: pas Gauss toe en vind dat de schil er nog niet toe doet.
Tussen R1 en R2: een doordenkertje. Het elektrisch veld in de geleider is nul. Dat is als volgt in te zien: in de geleider kan de (negatieve) lading bewegen. Als er een veld zou zijn, zou dat ook gebeuren. De lading zou net zo lang bewegen tot de nieuwe ladingsverdeling zo is, dat er geen veld binnen de geleider is.
Voorbij R2: de totale omsloten lading is weer gewoon Q, het veld valt af alsof er een puntlading Q in het midden zit.
f) De ingesloten lading vind je door ρ te integreren: ![[Graphics:Images/e+m2_gr_106.gif]](Images/e+m2_gr_106.gif) = 4 π
= 4 π ![[Graphics:Images/e+m2_gr_107.gif]](Images/e+m2_gr_107.gif) = 4 π
= 4 π ![[Graphics:Images/e+m2_gr_108.gif]](Images/e+m2_gr_108.gif) (
( ![[Graphics:Images/e+m2_gr_109.gif]](Images/e+m2_gr_109.gif) -
- ![[Graphics:Images/e+m2_gr_110.gif]](Images/e+m2_gr_110.gif) ). De situatie is bolsymmetrisch, dus de uitkomst voor het elektrisch veld vind je door te delen door 4π
). De situatie is bolsymmetrisch, dus de uitkomst voor het elektrisch veld vind je door te delen door 4π![[Graphics:Images/e+m2_gr_111.gif]](Images/e+m2_gr_111.gif)
![[Graphics:Images/e+m2_gr_112.gif]](Images/e+m2_gr_112.gif) : E(r)=
: E(r)=![[Graphics:Images/e+m2_gr_113.gif]](Images/e+m2_gr_113.gif) (
(![[Graphics:Images/e+m2_gr_114.gif]](Images/e+m2_gr_114.gif) -
-![[Graphics:Images/e+m2_gr_115.gif]](Images/e+m2_gr_115.gif) ). Voor r>R heb je weer het veld van een lading Q (zie opdracht 8 d) voor een uitdrukking voor Q).
). Voor r>R heb je weer het veld van een lading Q (zie opdracht 8 d) voor een uitdrukking voor Q).
g) De totale lading die op het boloppervlak met straal R1 zit, is -Q. Dat is als volgt in te zien. Neem als Gaussvolume een bol met een straal r tussen R1 en R2 in. De integraal wordt gelijk aan EO, en dat is 0, want E is nul (zie e)). Als die integraal nul is, moet de totale omsloten lading nul zijn. als er +Q in de oorsprong zit, moet de totale lading op het "binnen-opppervlak" gelijk zijn aan -Q. De oppervlaktelading is dan ![[Graphics:Images/e+m2_gr_116.gif]](Images/e+m2_gr_116.gif)
![[Graphics:Images/e+m2_gr_117.gif]](Images/e+m2_gr_117.gif)
![[Graphics:Images/e+m2_gr_118.gif]](Images/e+m2_gr_118.gif)
![[Graphics:Images/e+m2_gr_119.gif]](Images/e+m2_gr_119.gif)
Dit is de grafiek die hoort bij een puntlading. Bij c) is de waarde eerst nul en begint de grafiek bij R (de grafiek loopt verder hetzelfde). Bij d) loopt de grafiek vanuit 0 lineair omhoog tot r=R, vanaf daar volgt de grafiek de bovenstaande grafiek. Bij e) heb je ook dezelfde grafiek, met een onderbreking voor ![[Graphics:Images/e+m2_gr_120.gif]](Images/e+m2_gr_120.gif) <r<
<r<![[Graphics:Images/e+m2_gr_121.gif]](Images/e+m2_gr_121.gif) . In dat stuk is de waarde 0. De grafiek valt dus plotseling omlaag bij r=
. In dat stuk is de waarde 0. De grafiek valt dus plotseling omlaag bij r=![[Graphics:Images/e+m2_gr_122.gif]](Images/e+m2_gr_122.gif) , en springt terug naar de oude grafiek bij r=
, en springt terug naar de oude grafiek bij r=![[Graphics:Images/e+m2_gr_123.gif]](Images/e+m2_gr_123.gif) .
.
h) Als het elektrisch veld toeneemt met de tweede macht, moet de flux, dus E*oppervlak van de bolschil, toenemen met de vierde macht. Als je goed rekening houdt met de Jacobiaan (extra factor ![[Graphics:Images/e+m2_gr_124.gif]](Images/e+m2_gr_124.gif) in de integraal), vind je dat de ladingsdichtheid evenredig is met r.
in de integraal), vind je dat de ladingsdichtheid evenredig is met r.
Opdracht 14
De bedrage van een sector van de ring is gegeven door zijn lading dQ keer de afstand d tot het punt P in het quadraat
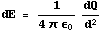
De lading van de sector is gegeven door:
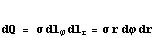
De afstand is gegeven door:
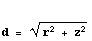
Doordat ons testpunt zich precies in het midden (r = 0) boven de schijf bevindt, draagt alleen de z-komponent van onze sector bij tot het E veld bij tot het E-veld in P.
De grootte van de z-komponent kunnen we met behulp van de cosinus regel berekenen.
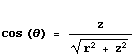
Hier mee vinden we dus volgende bijdrage van onze sector tot het totale E-veld in P:
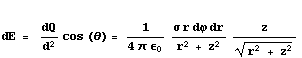
Het integraal dat we uit moeten rekenen is dus gegeven door het integraal van dE over het gehele oppervlakte van de schrijf. Dus van 0 < ϕ < 2π voor ϕ en van 0 < r < R voor r.
![E _ z = Underscript[∫, opp] dE = Underoverscript[∫, 0, arg3] Underoverscript[∫, 0, arg3] (z σ)/(4 π ϵ _ 0) r/(r^2 + z^2)^3^(1/2) dϕ dr = (z σ)/(2 ϵ _ 0) Underoverscript[∫, 0, arg3] r/(r^2 + z^2)^3^(1/2) dr = (z σ)/(2 ϵ _ 0)[-1/(r^2 + z^2)^(1/2)] _ 0^R = (z σ)/(2 ϵ _ 0) (1 - z/(R^2 + z^2)^(1/2))](HTMLFiles/vraag14_6.gif)
Het E-veld is dus gegeven door de grootte van de z-komponent maal de eenheidsvector in richting van z.
![Overscript[E, →] = σ/(2 ϵ _ 0) (1 - z/(R^2 + z^2)^(1/2)) Overscript[z,^]](HTMLFiles/vraag14_7.gif)
We bekijken nu het veld voor z << R en z >> R.
Voor z << R geldt dat de bijdrage van de tweede term verdwijnt:
![RowBox[{, RowBox[{Overscript[E, →], , =, , RowBox[{(z σ)/(2 ϵ _ 0), Overscript[z,^], , Cell[TextData[voor z << R]]}]}]}]](HTMLFiles/vraag14_8.gif)
We zien dus dat het veld er voor hele kleine afstanden net zo uitziet als het veld van een plaat kondensator, precies zoals we het verwacht hadden.
Voor z >> R moeten we uitdrukking voor E nog een beetje omschrijfen, omdat het niet meteen duidelijk is wat de uitdrukking tussen de haken doet.
![Overscript[E, →] = ( σ)/(2 ϵ _ 0) (1 - z/(R^2 + z^2)^(1/2)) = σ/(2 ϵ _ 0) (R^2 + z^2 - z (R^2 + z^2)^(1/2))/(R^2 + z^2) = σ/(2 ϵ _ 0) ( R^2 /(R^2 + z^2) + (z^2 - z (R^2 + z^2)^(1/2))/(R^2 + z^2))](HTMLFiles/vraag14_9.gif)
Als we nu de limiet z >> R kiezen, dan gaat de tweede term tegen 0 en blijft dus alleen de eerste over.
![2 RowBox[{Overscript[E, →], , =, , RowBox[{σ/(2 ϵ _ 0), , R^2 /z^2, Cell[TextData[{met Q = 2π, Cell[BoxData[R σ]]}]]}]}] = Q/(4 π ϵ _ 0) 1/z^2](HTMLFiles/vraag14_10.gif)
Voor hele grote afstanden ziet het veld er dus net zo uit als dat van een puntlading!
Converted by Mathematica
June 24, 2003
![[Graphics:Images/e+m2_gr_49.gif]](Images/e+m2_gr_49.gif)
![[Graphics:Images/e+m2_gr_119.gif]](Images/e+m2_gr_119.gif)
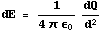
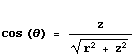
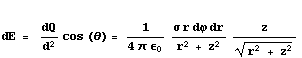
![E _ z = Underscript[∫, opp] dE = Underoverscript[∫, 0, arg3] Underoverscript[∫, 0, arg3] (z σ)/(4 π ϵ _ 0) r/(r^2 + z^2)^3^(1/2) dϕ dr = (z σ)/(2 ϵ _ 0) Underoverscript[∫, 0, arg3] r/(r^2 + z^2)^3^(1/2) dr = (z σ)/(2 ϵ _ 0)[-1/(r^2 + z^2)^(1/2)] _ 0^R = (z σ)/(2 ϵ _ 0) (1 - z/(R^2 + z^2)^(1/2))](HTMLFiles/vraag14_6.gif)
![Overscript[E, →] = σ/(2 ϵ _ 0) (1 - z/(R^2 + z^2)^(1/2)) Overscript[z,^]](HTMLFiles/vraag14_7.gif)
![RowBox[{, RowBox[{Overscript[E, →], , =, , RowBox[{(z σ)/(2 ϵ _ 0), Overscript[z,^], , Cell[TextData[voor z << R]]}]}]}]](HTMLFiles/vraag14_8.gif)
![Overscript[E, →] = ( σ)/(2 ϵ _ 0) (1 - z/(R^2 + z^2)^(1/2)) = σ/(2 ϵ _ 0) (R^2 + z^2 - z (R^2 + z^2)^(1/2))/(R^2 + z^2) = σ/(2 ϵ _ 0) ( R^2 /(R^2 + z^2) + (z^2 - z (R^2 + z^2)^(1/2))/(R^2 + z^2))](HTMLFiles/vraag14_9.gif)
![2 RowBox[{Overscript[E, →], , =, , RowBox[{σ/(2 ϵ _ 0), , R^2 /z^2, Cell[TextData[{met Q = 2π, Cell[BoxData[R σ]]}]]}]}] = Q/(4 π ϵ _ 0) 1/z^2](HTMLFiles/vraag14_10.gif)