Opdracht 7
a) Niet waar, het inprodukt van twee vektoren is een getal.
b) Omdat |![Overscript[r,^]](HTMLFiles/e+m_1.gif) | = 1 geldt:
| = 1 geldt:
![Overscript[a, ->] Overscript[r,^]](HTMLFiles/e+m_2.gif) = |
= |![Overscript[a, ->]](HTMLFiles/e+m_3.gif) | |
| |![Overscript[r,^]](HTMLFiles/e+m_4.gif) | cos(
| cos(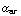 ) = |
) = |![Overscript[a, ->]](HTMLFiles/e+m_6.gif) | cos(
| cos(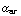 ).
).
Dit is de component van ![Overscript[a, ->]](HTMLFiles/e+m_8.gif) in de richting van
in de richting van ![Overscript[r,^]](HTMLFiles/e+m_9.gif) .
.
c) Met d![Overscript[n, ->]](HTMLFiles/e+m_10.gif) wordt bedoeld
wordt bedoeld ![Overscript[n, ->]](HTMLFiles/e+m_11.gif) dO. Als je nu invult
dO. Als je nu invult ![Overscript[E, ->]](HTMLFiles/e+m_12.gif) =
= ![Overscript[n, ->]](HTMLFiles/e+m_13.gif) krijg je:
krijg je:
![∫ _ O Overscript[E, ->] * d Overscript[n, ->]](HTMLFiles/e+m_14.gif) =
= ![∫ _ O Overscript[n, ->] * Overscript[n, ->] d](HTMLFiles/e+m_15.gif) O =
O = 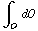 = O.
= O.
Opdracht 8
a) Totale lading: Q = 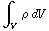 = ρ
= ρ 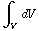 = ρ
= ρ 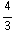 π
π 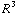 .
.
b) Het gemiddelde van ρ (r) is 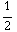
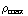 , dus je zou misschien denken dat de totale lading
, dus je zou misschien denken dat de totale lading
twee keer zo klein is.
c) ρ (r) = a*r + b, met ρ (0) = 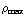 en ρ (R) = 0. Oplossen levert: b =
en ρ (R) = 0. Oplossen levert: b = 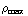 en a = -
en a = -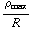 .
.
d) Q = 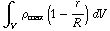 =
= 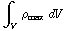 -
- 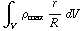 =
= 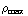
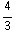 π
π 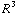 -
- 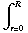
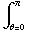
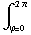
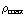
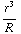 sin θ dr dθ dϕ .
sin θ dr dθ dϕ .
De integralen over θ en ϕ leveren een factor 4π, de integraal over r wordt 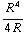 =
= 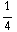
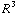 . Uiteindelijk krijgen we dan:
. Uiteindelijk krijgen we dan:
Q = 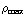
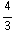 π
π 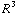 -
- 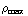 π
π 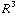 =
= 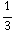
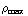 π
π 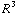 .
.
e) De totale lading is dus vier keer zo klein geworden, en niet twee keer. Dit kun je verklaren door te bedenken dat de inhoud van een bolschilletje met dikte dr, 4π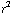 dr is. Hoe groter r, des te groter dus deze inhoud, en des te groter ook de bijdrage aan de integraal. Dit zorgt ervoor dat de integraal meer dan twee keer zo klein wordt, immers ρ(r) is klein voor grote r.
dr is. Hoe groter r, des te groter dus deze inhoud, en des te groter ook de bijdrage aan de integraal. Dit zorgt ervoor dat de integraal meer dan twee keer zo klein wordt, immers ρ(r) is klein voor grote r.
Opdracht 9
a)
![[Graphics:HTMLFiles/e+m_49.gif]](HTMLFiles/e+m_49.gif)
b) Voor de flux geldt: φ = ![∫ _ A Overscript[E, ->] * Overscript[n, ->] dA](HTMLFiles/e+m_50.gif) . In de figuur zien we dat
. In de figuur zien we dat ![Overscript[E, ->]](HTMLFiles/e+m_51.gif) altijd loodrecht op het oppervlak staat, dus
altijd loodrecht op het oppervlak staat, dus ![Overscript[E, ->] * Overscript[n, ->]](HTMLFiles/e+m_52.gif) = |
= |![Overscript[E, ->]](HTMLFiles/e+m_53.gif) |. Verder is de afstand tot de oorsprong constant op het oppervlak, en dus is de grootte van
|. Verder is de afstand tot de oorsprong constant op het oppervlak, en dus is de grootte van ![Overscript[E, ->]](HTMLFiles/e+m_54.gif) ook constant want die hangt alleen van |
ook constant want die hangt alleen van |![Overscript[r, ->]](HTMLFiles/e+m_55.gif) | af. We krijgen dus:
| af. We krijgen dus:
φ = E 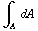 =
= 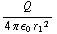
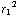 sin
sin 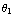
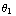
c) Als er 'iets' is wat door een oppervlak gaat, kun je spreken van flux. Bij licht gaat het om fotonen, bij geluid om geluidsgolven, en bij een radioactieve bron om radioactieve deeltjes.
d) Er geldt: 0,01*h=0,01*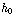 +
+ 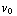 t +
t + 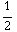 a
a 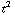 (h is in centimeters, vandaar de factoren 0,01). We weten:
(h is in centimeters, vandaar de factoren 0,01). We weten: 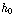 = 0 m,
= 0 m, 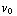 = 0,1 m/s, en a = 9,8 m/
= 0,1 m/s, en a = 9,8 m/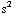 . Als we hieruit t oplossen krijgen we:
. Als we hieruit t oplossen krijgen we:
t=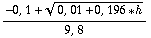 . (we willen dat t>0 , dus de negatieve oplossing doet niet mee)
. (we willen dat t>0 , dus de negatieve oplossing doet niet mee)
Verder weten we v = 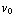 + a*t = 0,1 + 9,8 t . Vullen we t in dan vinden we: v =
+ a*t = 0,1 + 9,8 t . Vullen we t in dan vinden we: v = 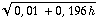 .
.
e) Als de fluxen elkaar niet opheffen dan neemt de hoeveelheid water in de straal toe of af. Dit kan natuurlijk niet eeuwig doorgaan; na verloop van tijd moet de hoeveelheid water constant blijven, oftewel de fluxen zijn gelijk.
f) De flux is hier de hoeveelheid water die per seconde door het oppervlak stroomt. Dit is gelijk aan A*v, oppervlakte keer snelheid (merk op, dit heeft de dimensie 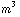 / s, inderdaad dus een hoeveelheid per seconde). De diameter van de straal bij h=0 is 1 cm. De flux aldaar moet gelijk zijn aan de flux op een hoogte h. We krijgen dan:
/ s, inderdaad dus een hoeveelheid per seconde). De diameter van de straal bij h=0 is 1 cm. De flux aldaar moet gelijk zijn aan de flux op een hoogte h. We krijgen dan:
π * 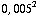 * 0,1 = π *
* 0,1 = π * 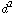 *
* 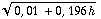 .
.
Als we hieruit d oplossen krijgen we
d = 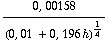
Opdracht 10
a) Om de wet van Gauss toe te passen moet je de oppervlakte-integraal ![∫ _ A Overscript[E, ->] * Overscript[n, ->] dA](HTMLFiles/e+m_76.gif) uitrekenen, met A een gesloten oppervlak waar het geladen voorwerp zich in bevindt. Deze integraal is alleen makkelijk uit te rekenen als er een symmetrie in het systeem zit. De drie symmetrieen die 'werken' zijn: sferische symmetrie, vlaksymmetrie, en cylindrische symmetrie. Zie ook bijv. Griffiths p. 71. Een geladen bal (lading Q) is sferisch symmetrisch, dit gaat dus werken. Kies voor A een bolschil om de bal heen, dan is
uitrekenen, met A een gesloten oppervlak waar het geladen voorwerp zich in bevindt. Deze integraal is alleen makkelijk uit te rekenen als er een symmetrie in het systeem zit. De drie symmetrieen die 'werken' zijn: sferische symmetrie, vlaksymmetrie, en cylindrische symmetrie. Zie ook bijv. Griffiths p. 71. Een geladen bal (lading Q) is sferisch symmetrisch, dit gaat dus werken. Kies voor A een bolschil om de bal heen, dan is ![Overscript[E, ->] * Overscript[n, ->]](HTMLFiles/e+m_77.gif) overal op de bolschil constant en kunnen we dat dus buiten de integraal halen. Uit de stelling van Gauss volgt dan:
overal op de bolschil constant en kunnen we dat dus buiten de integraal halen. Uit de stelling van Gauss volgt dan:
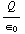 =
= ![∫ _ A Overscript[E, ->] * Overscript[n, ->] dA](HTMLFiles/e+m_79.gif) = E
= E 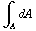 = E 4 π
= E 4 π 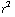 ,
,
E = 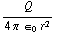 .
.
b) Een schoen is zeker niet symmetrisch, we hebben dus weinig aan de stelling van Gauss.
c) Van een oneindig grote plaat kun je eenvoudig met de stelling van Gauss het veld berekenen (het systeem heeft vlaksymmetrie). Zie p. 49 van de transparanten. Je vindt: E = 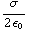 .
.
Het veld van een dozijn platen kun je dan vinden door de bijdrage van elke plaat afzonderlijk op te tellen (superpositiebeginsel).
d) Een kubus heeft niet een van de drie symmetrieen bij a). Gauss helpt dus hier niet.
Opdracht 12
a) 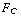 =
= 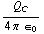 (
( 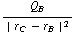 +
+ 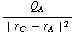 ), en evenzo voor de andere ladingen (de krachten op B zijn natuurlijk wel tegengesteld).
), en evenzo voor de andere ladingen (de krachten op B zijn natuurlijk wel tegengesteld).
b) Het veld op x = 1 cm: E = | - 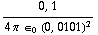 +
+ 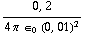 -
- 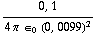 | = 5,4
| = 5,4 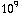 N / C. Evenzo vinden we 3,37
N / C. Evenzo vinden we 3,37 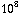 N / C op x = 2 cm, en
N / C op x = 2 cm, en
6,66 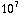 N / C op x = 3 cm. De waarde bij x = 2 cm is 16 =
N / C op x = 3 cm. De waarde bij x = 2 cm is 16 = 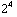 keer zo klein als die voor x = 1 cm, terwijl x 2 keer zo groot is. En de waarde bij x = 3 cm is 81 =
keer zo klein als die voor x = 1 cm, terwijl x 2 keer zo groot is. En de waarde bij x = 3 cm is 81 = 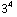 keer zo klein als die voor x = 1 cm. Het veld neemt dus af met
keer zo klein als die voor x = 1 cm. Het veld neemt dus af met 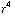 .
.
c) Omdat in een watermolecuul een knik zit, is er een positieve kant (waar de waterstofatomen zitten) en een negatieve kant (waar het zuurstofatoom zit). Dit is dus een dipool, het veld valt af met de derde macht. Koolstofdioxide lijkt meer op de configuratie van vraag B, het molecuul is recht. Het veld zal afvallen met de vierde macht.
Opdracht 13
a) Nee dat kan niet. Mocht je denken dat je vanwege de wet van Gauss alleen te maken hebt met de lading die dichter bij de oorsprong ligt dan het punt waarin je kijkt, dan vergeet je dat de wet van Gauss alleen iets zegt over de bijdrage van een lading aan de oppervlakte-integraal van de normale component van het elektrisch veld. Dat de bijdrage van een lading aan de integraal nul is, wil niet zeggen dat de bijdrage in elk punt nul is.
b) Een puntlading is een standaardgeval: E = 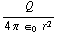 .
.
c) Het veld is in ieder geval naar buiten gericht en in grootte alleen afhankelijk van de afstand tot het middelpunt. De oppervlakte-integraal die in de wet van Gauss vookomt is dus gelijk aan EO. Zolang het boloppervlak O binnen de bolschil ligt, is er geen omsloten lading. EO is dan nul, en omdat O geen nul is, is E nul (dit kan alleen omdat je weet dat het veld radieel is, alleen daardoor weet je dat de integraal EO is). Buiten de bolschil is de omsloten lading gelijk aan de totale lading. Het verloop is verder net zo als wanneer alle lading in het middelpunt van de bolschil had gezeten.
d) Neem een boloppervlak O met straal r (<R ). Om de ingesloten lading te bepalen moeten we ρ integreren tot aan r: 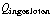 = 4 π
= 4 π 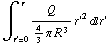 = Q
= Q 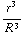 . We weten weer dat E loodrecht op het oppervlak staat en alleen van |r| afhangt, dus
. We weten weer dat E loodrecht op het oppervlak staat en alleen van |r| afhangt, dus ![∫ _ O Overscript[E, ->] * Overscript[dA, ->]](HTMLFiles/e+m_101.gif) = E 4 π
= E 4 π 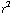 . We vinden dus: E =
. We vinden dus: E = 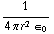 Q
Q 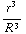 =
= 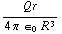 .
.
Buiten de bol is het veld weer net zoals dat van een puntlading Q.
e) Dit is duidelijk weer een radieel probleem. De integraal komt weer neer op EO, de waarde maal de oppervlakte.
Tot R1: pas Gauss toe en vind dat de schil er nog niet toe doet.
Tussen R1 en R2: een doordenkertje. Het elektrisch veld in de geleider is nul. Dat is als volgt in te zien: in de geleider kan de (negatieve) lading bewegen. Als er een veld zou zijn, zou dat ook gebeuren. De lading zou net zo lang bewegen tot de nieuwe ladingsverdeling zo is, dat er geen veld binnen de geleider is.
Voorbij R2: de totale omsloten lading is weer gewoon Q, het veld valt af alsof er een puntlading Q in het midden zit.
f) De ingesloten lading vind je door ρ te integreren: 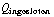 = 4 π
= 4 π 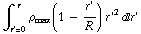 = 4 π
= 4 π 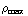 (
( 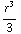 -
- 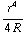 ). De situatie is bolsymmetrisch, dus de uitkomst voor het elektrisch veld vind je door te delen door 4π
). De situatie is bolsymmetrisch, dus de uitkomst voor het elektrisch veld vind je door te delen door 4π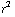
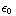 : E(r)=
: E(r)=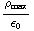 (
(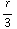 -
-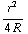 ). Voor r>R heb je weer het veld van een lading Q (zie opdracht 8 d) voor een uitdrukking voor Q).
). Voor r>R heb je weer het veld van een lading Q (zie opdracht 8 d) voor een uitdrukking voor Q).
g) De totale lading die op het boloppervlak met straal R1 zit, is -Q. Dat is als volgt in te zien. Neem als Gaussvolume een bol met een straal r tussen R1 en R2 in. De integraal wordt gelijk aan EO, en dat is 0, want E is nul (zie e)). Als die integraal nul is, moet de totale omsloten lading nul zijn. als er +Q in de oorsprong zit, moet de totale lading op het "binnen-opppervlak" gelijk zijn aan -Q. De oppervlaktelading is dan 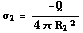
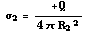
![Plot[1/r^2, {r, .5, 5}] ;](HTMLFiles/e+m_118.gif)
![[Graphics:HTMLFiles/e+m_119.gif]](HTMLFiles/e+m_119.gif)
Dit is de grafiek die hoort bij een puntlading. Bij c) is de waarde eerst nul en begint de grafiek bij R (de grafiek loopt verder hetzelfde). Bij d) loopt de grafiek vanuit 0 lineair omhoog tot r=R, vanaf daar volgt de grafiek de bovenstaande grafiek. Bij e) heb je ook dezelfde grafiek, met een onderbreking voor 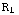 <r<
<r<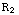 . In dat stuk is de waarde 0. De grafiek valt dus plotseling omlaag bij r=
. In dat stuk is de waarde 0. De grafiek valt dus plotseling omlaag bij r=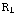 , en springt terug naar de oude grafiek bij r=
, en springt terug naar de oude grafiek bij r=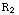 .
.
h) Als het elektrisch veld toeneemt met de tweede macht, moet de flux, dus E*oppervlak van de bolschil, toenemen met de vierde macht. Als je goed rekening houdt met de Jacobiaan (extra factor 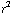 in de integraal), vind je dat de ladingsdichtheid evenredig is met r.
in de integraal), vind je dat de ladingsdichtheid evenredig is met r.
Opdracht 9
De divergentie van een vectorveld moet een scalar opleveren. Het antwoord is 2x-4y+6z.
Opdracht 11
a) ![Overscript[E, ->]](HTMLFiles/e+m_125.gif) =
= 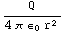
![Overscript[r,^]](HTMLFiles/e+m_127.gif) (zie opdracht 13 van dagdeel 2).
(zie opdracht 13 van dagdeel 2).
b) De divergentie van het E-veld geeft de ladingsdichtheid (gedeeld door 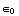 ). Buiten de bol is de ladingsdichtheid 0, dus dan moet de divergentie van
). Buiten de bol is de ladingsdichtheid 0, dus dan moet de divergentie van ![Overscript[E, ->]](HTMLFiles/e+m_129.gif) daar ook 0 zijn.
daar ook 0 zijn.
c) We laten de constante 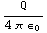 even buiten beschouwing. Dan is de x-component van
even buiten beschouwing. Dan is de x-component van ![Overscript[E, ->]](HTMLFiles/e+m_131.gif) gelijk aan
gelijk aan 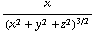 . De afgeleide naar x van de x-component levert:
. De afgeleide naar x van de x-component levert: 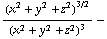
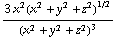 . De y en de z-component leveren (met de regel voor het nemen van de afgeleide van een quotient) steeds dezelfde eerste term, en respectievelijk -
. De y en de z-component leveren (met de regel voor het nemen van de afgeleide van een quotient) steeds dezelfde eerste term, en respectievelijk -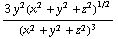 en -
en -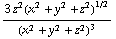 . Die "laatste termen" samen leveren -3
. Die "laatste termen" samen leveren -3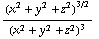 en vallen weg tegen de drie termen
en vallen weg tegen de drie termen 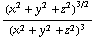 .
.
d) Bij deze opgave is het handig om te gebruiken dat ![Overscript[∂, ->] * Overscript[r, ->]](HTMLFiles/e+m_139.gif) = 1+1+1 = 3. Verder is
= 1+1+1 = 3. Verder is ![Overscript[∂, ->] r](HTMLFiles/e+m_140.gif) =
= ![Overscript[r, ∧]](HTMLFiles/e+m_141.gif) (ga na!). Schrijf nu eerst het E-veld om van
(ga na!). Schrijf nu eerst het E-veld om van ![Overscript[r, ∧]](HTMLFiles/e+m_142.gif) naar
naar ![Overscript[r, ->]](HTMLFiles/e+m_143.gif) :
:
![Overscript[E, ->]](HTMLFiles/e+m_144.gif) =
= 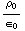 (
(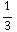 -
- 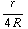 )
) ![Overscript[r, ->]](HTMLFiles/e+m_148.gif) ,
,
ρ = 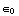
![Overscript[∂, ->] * Overscript[ E, ->]](HTMLFiles/e+m_150.gif) =
= 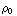
![Overscript[∂, ->]](HTMLFiles/e+m_152.gif) * (
* (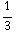 -
- 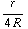 )
) ![Overscript[r, ->]](HTMLFiles/e+m_155.gif) =
= 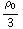
![Overscript[∂, ->] * Overscript[r, ->]](HTMLFiles/e+m_157.gif) -
- 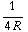
![Overscript[∂ *, ->] (r Overscript[r, ->])](HTMLFiles/e+m_159.gif) =
= 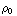 -
- 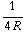 ( r (
( r (![Overscript[∂, ->] * Overscript[ r, ->]](HTMLFiles/e+m_162.gif) ) +
) + ![Overscript[r, ->]](HTMLFiles/e+m_163.gif) * (
* (![Overscript[∂, ->] r ) )](HTMLFiles/e+m_164.gif) =
= 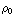 -
- 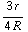 -
- 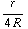 =
= 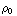 ( 1 -
( 1 - 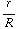 ).
).
e) In opdracht 13 werd de wet van Gauss in integraalvolm gebruikt om te laten zien dat bij deze ladingsverdeling dit elektrisch veld hoort. Maar goed dat je met de wet van Gauss in differentiele vorm uit dit elektrisch veld weer deze ladinsverdeling krijgt.
Opdracht 13
a) In het midden wordt het veld uit een hoekpunt precies opgeheven door het veld uit het hoekpunt aan de overkant. De netto veldsterkte is dus 0.
b) De potentiaal van een puntlading is: V = 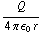 . We moeten nu de bijdragen van de vier ladingen bij elkaar optellen. Omdat de afstand tussen het middelpunt en de hoeken steeds hetzelfde is (namelijk
. We moeten nu de bijdragen van de vier ladingen bij elkaar optellen. Omdat de afstand tussen het middelpunt en de hoeken steeds hetzelfde is (namelijk 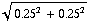 =
= 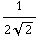 ) , zijn de bijdragen ook gelijk. Je krijgt:
) , zijn de bijdragen ook gelijk. Je krijgt:
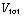 = 4 *
= 4 * 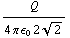 = 2 *
= 2 * 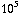 V
V
c) Je kunt de configuratie opbouwen door de ladingen een voor een vanuit het oneindige op de goede plaats te zetten. De eerste lading kun je neerzetten zonder dat het energie kost (hij 'voelt' nog geen elektrisch veld). De tweede wordt afgestoten door de eerste, de energie die het kost om hem op afstand a van de eerste lading te brengen is Q * V(a), met V(a) de potentiaal van de eerste lading op afstand a. De derde lading ondervindt de potentialen van de eerste twee ladingen, de benodigde energie is Q * ( V(a) + V(a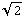 ) ). Bij de vierde lading zijn er drie bijdragen, de energie is Q * ( V(a) + V(a
) ). Bij de vierde lading zijn er drie bijdragen, de energie is Q * ( V(a) + V(a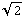 ) + V(a) ). In totaal krijgen we dan: U = Q * ( 4*V(a) + 2*V(a
) + V(a) ). In totaal krijgen we dan: U = Q * ( 4*V(a) + 2*V(a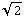 ) ) = 0,39 J.
) ) = 0,39 J.
Opdracht 14
a) In het begin hebben beide bollen lading +Q. Omdat de stralen verschillend zijn, zijn de potentialen verschillend (de grootste bol heeft de laagste potentiaal). Als de bollen verbonden worden, zal er lading van hoge naar lage potentiaal stromen (of negatieve lading van lage naar hoge potentiaal, dat komt op hetzelfde neer.) Dit gaat door tot de potentialen gelijk zijn. Er komt dus meer lading op de grote bol en minder op de kleine.
b) De potentialen zijn gelijk, dus 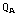 /(
/( )=
)= 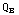 /(
/( )
)
De veldsterktes net buiten de bollen worden gegeven door 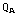 /(
/(
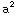 ) respectievelijk
) respectievelijk 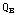 /(
/(
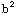 ) . Dat is een factor 1/a respectievelijk 1/b ten opzichte van de uitdrukkingen voor de potentialen. Omdat de potentialen gelijk zijn, geldt
) . Dat is een factor 1/a respectievelijk 1/b ten opzichte van de uitdrukkingen voor de potentialen. Omdat de potentialen gelijk zijn, geldt 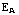 :
: 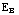 =1/a : 1/b. Bij de kleinste straal is de waarde het grootst. Als je een spitse punt voorstelt door een bolletje met een kleine straal, blijkt het veld groot te zijn.
=1/a : 1/b. Bij de kleinste straal is de waarde het grootst. Als je een spitse punt voorstelt door een bolletje met een kleine straal, blijkt het veld groot te zijn.
Merk op dat als de ladingen niet zouden zijn veranderd het veld bij de kleine bol nog groter en dat dat bij de grote bol nog kleiner zou zijn. Om te illustreren hoe het gaat bij de scherpe punt van een geleider, moet je echter de situatie beschouwen waarbij de verbinding is gemaakt.
Opdracht 15
a) De gradient van een functie wijst in de richting waarin de functie het sterkst toeneemt. De gegeven potentiaal verandert alleen als functie van |![Overscript[r, ->]](HTMLFiles/e+m_191.gif) |, dus zal
|, dus zal ![Overscript[E, ->]](HTMLFiles/e+m_192.gif) (= -
(= -![Overscript[∂, ->] V](HTMLFiles/e+m_193.gif) ) in de
) in de ![Overscript[r, ∧]](HTMLFiles/e+m_194.gif) -richting wijzen.
-richting wijzen.
b) Kettingregel gebruiken: ![Overscript[E, ->]](HTMLFiles/e+m_195.gif) = -
= -![Overscript[∂, ->] V](HTMLFiles/e+m_196.gif) = -
= -![Overscript[∂, ->] r^(7/2)](HTMLFiles/e+m_197.gif) = -
= -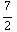
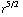 (
( ![Overscript[∂, ->]](HTMLFiles/e+m_200.gif) r ) = -
r ) = -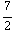
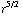
![Overscript[r, ∧]](HTMLFiles/e+m_203.gif) .
.
c) ρ = 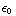
![Overscript[∂, ->] * Overscript[ E, ->]](HTMLFiles/e+m_205.gif) = -
= -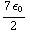
![Overscript[∂, ->]](HTMLFiles/e+m_207.gif) * (
* ( 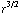
![Overscript[r, ->]](HTMLFiles/e+m_209.gif) ) = -
) = -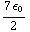 (
( 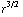 (
( ![Overscript[∂, ->]](HTMLFiles/e+m_212.gif) *
* ![Overscript[r, ->]](HTMLFiles/e+m_213.gif) ) +
) + ![Overscript[r, ->]](HTMLFiles/e+m_214.gif) * (
* ( ![Overscript[∂, ->]](HTMLFiles/e+m_215.gif) (
( 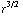 ) ) ) = -
) ) ) = -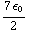 ( 3
( 3 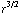 +
+ 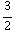
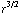 ) = -
) = -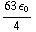
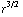 .
.
d) Integreer ![Overscript[E, ->]](HTMLFiles/e+m_223.gif) over een bolschil met straal r: 4 π
over een bolschil met straal r: 4 π 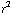 E =
E = ![∫ _ A Overscript[E, ->] * d Overscript[A, ->]](HTMLFiles/e+m_225.gif) =
= 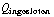 /
/ 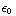 = -
= -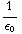
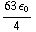 4 π
4 π 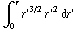 = 63 π
= 63 π 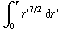
= - 63 π 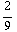
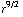 .
.
Hieruit vinden we dus voor E: E = - 63 π 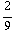
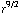
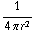 = -
= -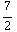
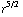 . Klopt met a).
. Klopt met a).
Opdracht 9
C =Q/V. Als er een lading +Q, respectievelijk -Q op de platen zit, en er is een dielektricum aanwezig, dan ontstaat een negatieve polarisatielading aan de kant van +Q en een negatieve polarisatielading aan de -Q kant. Het veld tussen de platen is kleiner, het potentiaalverschil dus ook. C=Q/V is dus groter.
Opdracht 10
qE is de kracht, D is slechts een hulpveld.
Opdracht 11
a) Neem een kring, met de lange zijden aan weerszijden van de grens, en hele korte zijden loodrecht daarop. Omdat de kringintegraal van het elektrisch veld nul is, omdat de infinitesimaal korte zijden geen bijdragen geven, en omdat de twee lange zijden in tegengestelde richting worden doorlopen, volgt dat de component van het elektrisch veld parallel aan de grens aan weerszijden van de grens gelijk is (dat is automatisch niet zo voor het D veld, als E hetzelfde is en de materialen zijn verschillend, dan is de component van D niet gelijk. Er is ook geen wet die zegt dat de kringintegraal van D gelijk is aan nul.)
b) Neem nu een platte doos, met de grote oppervlakken aan weerszijden van het grensvlak. Omdat de vrije lading nul is, is de flux van het D-veld door het hele oppervlak nul. Omdat het randje infinitesimaal klein is, moeten de fluxen door boven- en ondervlak elkaar opheffen. Dit kan alleen voor elk oppervlak goed gaan als de loodrechte component boven en onder het grensvlak gelijk is (de ene keer wijst het naar buiten, de andere keer prikt het naar binnen, dus bij gelijke waarde van de loodrechte compnent, is de totale flux gelijk aan nul).
c/d V is gegeven. E is gelijk aan V/d, of er nu materiaal tussen zit of niet. Verder geldt 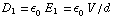 en
en 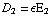 =
=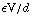 . We weten ook dat
. We weten ook dat 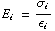 , dus
, dus 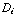 =
= 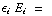
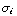 . Om de vrije lading te berekenen gebruik je Q =
. Om de vrije lading te berekenen gebruik je Q = 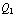 +
+ 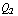 =
= 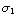
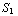 +
+ 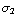
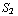 =
= 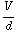 ( ϵ
( ϵ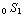 + ϵ
+ ϵ 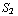 ). De capaciteit is nu C =
). De capaciteit is nu C = 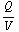 =
= 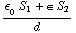 .
.
e/f Nu is Q gegeven. Dan volgt D = σ = Q/S. De elektrische velden zijn verschillend in beide delen: 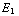 =
=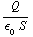 en
en 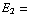
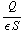 . De potentiaal vind je door te "integreren": V=
. De potentiaal vind je door te "integreren": V=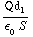 +
+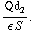
Ten slotte geldt C=Q/V. Daarvoor geldt 1/C=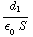 +
+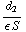 .
.
g) De wet van Snellius bepaalt hoe licht wordt gebroken. Dat licht wordt gebroken kun je nu grofweg als volgt inzien. Bekijk het E-veld bij de overgang tussen twee media, met 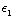 !=
!= 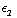 . Uit vraag a) weten we dat de component van E parallel aan het grensvlak continu is. Verder weten we dat de loodrechte component van D continu is. Maar dan is de loodrechte component van E niet continu, want
. Uit vraag a) weten we dat de component van E parallel aan het grensvlak continu is. Verder weten we dat de loodrechte component van D continu is. Maar dan is de loodrechte component van E niet continu, want 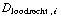 =
= 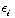
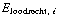 en de epsilons waren niet hetzelfde. De loodrechte component van E verandert dus, oftewel het E-veld wordt 'gebroken'.
en de epsilons waren niet hetzelfde. De loodrechte component van E verandert dus, oftewel het E-veld wordt 'gebroken'.
Opdracht 13
a) De dielektrische constante 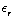 ( = 1 +
( = 1 + 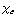 ) van papier is ongeveer 3. De uitdrukking voor de kracht is te vinden in de powerpointpresentatie, p. 118: F =
) van papier is ongeveer 3. De uitdrukking voor de kracht is te vinden in de powerpointpresentatie, p. 118: F = 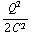
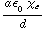 . Als je dit invult krijg je ongeveer 8 N. Merk op dat dit sterk van de afstand tussen de platen en de spanning afhangt.
. Als je dit invult krijg je ongeveer 8 N. Merk op dat dit sterk van de afstand tussen de platen en de spanning afhangt.
b) Voor de cylindercondensator moeten we de berekening van de kracht opnieuw doen. De capaciteit zonder tussenmedium is (zie ook opdracht 5 van dagdeel 1.5): C = - 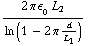 , met
, met 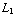 de diameter van de buitenste koker en
de diameter van de buitenste koker en 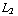 de lengte van de cylinder. Als de condensator gedeeltelijk wordt gevuld met een medium dan krijgen we voor de capaciteit: C = -
de lengte van de cylinder. Als de condensator gedeeltelijk wordt gevuld met een medium dan krijgen we voor de capaciteit: C = - 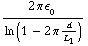 (
( 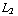 - x +
- x + 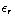 x ) = -
x ) = - 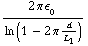 (
( 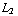 +
+ 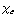 x ). De kracht wordt nu: F =
x ). De kracht wordt nu: F = 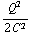
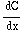 =
= 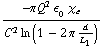 .
.
Opdracht 14
a) dU = V dq = 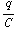 dq. Je kunt een ongeladen condensator (q = 0) opladen tot q = Q , door telkens stukjes dq toe te voegen. De daarvoor benodigde energie krijg je door alle bijdragen dU op te tellen, oftewel integreren:
dq. Je kunt een ongeladen condensator (q = 0) opladen tot q = Q , door telkens stukjes dq toe te voegen. De daarvoor benodigde energie krijg je door alle bijdragen dU op te tellen, oftewel integreren:
U = 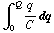 =
= 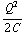 .
.
b) C = 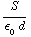 , dus U =
, dus U = 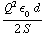 .
.
c) E is gelijk aan Q / (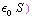 . Dit kwadrateren en vermenigvuldigen met het volume tussen de platen (en vermenigvuldigen met 1/2
. Dit kwadrateren en vermenigvuldigen met het volume tussen de platen (en vermenigvuldigen met 1/2 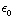 ) levert hetzelfde op als bij a.
) levert hetzelfde op als bij a.
d) De capaciteit vind je door Q/V te nemen (de potentiaal van een bol met lading Q en straal R is 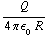 ). Daarna gebruik je a. Je vindt
). Daarna gebruik je a. Je vindt 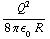 . Controle: merk op dat de dimensie dezelfde is als bij c.
. Controle: merk op dat de dimensie dezelfde is als bij c.
e) We moeten de energiedichtheid ( = 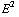 / 2
/ 2 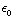 ) integreren over de hele ruimte. Binnen de bol is het veld 0, dat levert dus niets op. Buiten de bol is het veld
) integreren over de hele ruimte. Binnen de bol is het veld 0, dat levert dus niets op. Buiten de bol is het veld 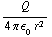 . We krijgen dus:
. We krijgen dus:
U = 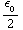
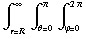
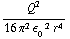
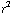 sin θ dr dθ dϕ =
sin θ dr dθ dϕ = 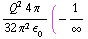 +
+ 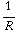 ) =
) = 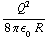 . Klopt met d.
. Klopt met d.
Opdracht 15
a) q(r)=4/3 πρ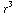 , V(r)=
, V(r)=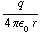 =
=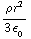 .
.
b) Vdq = V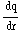 dr =
dr = 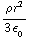 4π
4π 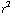 dr
dr
c) Integreer b) van 0 tot R: U = 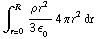 =
= 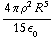 =
=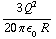
d) Je moet zowel het deel binnen als het deel buiten de bol meenemen. Het deel buiten de bol gaat precies hetzelfde als bij 14 e). Binnen de bol kriigen we De uitkomst is hetzelfde als bij i. De energie is groter dan bij de geleidende bol met dezelfde lading en straal, omdat er ook binnen de bol een veld is. De uitkomsten c) en d) zijn groter dan de uitkomsten 14 e) en f).
2.1.1
a) Je krijgt twee nieuwe magneten, die allebei een noord- en een zuidpool hebben.
b) en c) Papier en aluminium zijn nauwelijks magnetiseerbaar, de invloed op het externe veld (en dus op de magneten) is verwaarloosbaar.
d) Er is alleen een magnetische kracht op de lading als hij beweegt.
e) De snelheid en het veld staan parallel, de kracht is dus nul.
f) F = q v B. Met een handregel vind je dat de kracht van je af is gericht.
g) B = 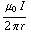 , met de kurketrekkerregel vind je dat het magneetveld rechts van de draad van je af is gericht.
, met de kurketrekkerregel vind je dat het magneetveld rechts van de draad van je af is gericht.
2.1.2
a) Regeltje bijvoorbeeld: vang de magnetische veldlijnen op in de palm van je linkerhand. Laat je vingers in de richting van de stroom wijzen. Je duim geeft dan de richting van de kracht. In dit geval is dat van je af.
b) ![Overscript[v, ->]](HTMLFiles/e+m_315.gif) = (0 , 0 , v) en
= (0 , 0 , v) en ![Overscript[B, ->]](HTMLFiles/e+m_316.gif) = (B , 0 , 0).
= (B , 0 , 0). ![Overscript[v, ->]](HTMLFiles/e+m_317.gif) ×
× ![Overscript[B, ->]](HTMLFiles/e+m_318.gif) = ( 0 , B v , 0 ). Dit is inderdaad van je af gericht.
= ( 0 , B v , 0 ). Dit is inderdaad van je af gericht.
2.1.3
a) Het B-veld staat in de z-richting en het deeltje beweegt in de x-richting.
b) m ![(d Overscript[v, ->])/(d t)](HTMLFiles/e+m_319.gif) = q
= q ![Overscript[v, ->]](HTMLFiles/e+m_320.gif) ×
× ![Overscript[B, ->]](HTMLFiles/e+m_321.gif)
c) 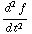 = -
= - 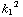
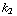 cos (
cos ( 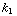 t ) = -
t ) = - 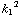 f (t)
f (t)
d) ![Overscript[v, ->]](HTMLFiles/e+m_327.gif) = (
= (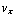 ,
, 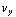 ,
, 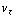 ) en
) en ![Overscript[B, ->]](HTMLFiles/e+m_331.gif) = (0 , 0 , B). Dus q
= (0 , 0 , B). Dus q ![Overscript[v, ->]](HTMLFiles/e+m_332.gif) ×
× ![Overscript[B, ->]](HTMLFiles/e+m_333.gif) = q (
= q ( 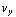 B , -
B , - 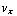 B , 0 ). De x-, y- en z-componenten van de krachtenvergelijking b) worden nu: m
B , 0 ). De x-, y- en z-componenten van de krachtenvergelijking b) worden nu: m 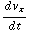 = q
= q 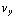 B , m
B , m 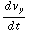 = - q
= - q 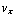 B , m
B , m 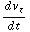 = 0. Uit de laatste vergelijking volgt
= 0. Uit de laatste vergelijking volgt 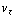 = constante, en de constante is nul omdat
= constante, en de constante is nul omdat 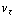 = 0 voor t = 0. Gebruik nu de tweede vergelijking om
= 0 voor t = 0. Gebruik nu de tweede vergelijking om 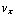 te elimineren in de eerste, en vice versa. Je krijgt: -
te elimineren in de eerste, en vice versa. Je krijgt: -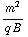
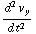 = q
= q 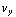 B, en -
B, en -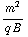
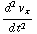 = q
= q 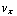 B. Dit lijkt op de vergelijking bij c), met
B. Dit lijkt op de vergelijking bij c), met 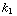 =
= 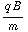 . We vinden dus:
. We vinden dus: 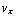 = α cos (
= α cos (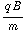 t ) + β sin (
t ) + β sin ( 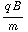 t ),
t ), 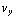 = γ cos (
= γ cos (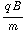 t ) + δ sin (
t ) + δ sin ( 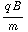 t ). Uit de beginvoorwaarde voor de snelheid (
t ). Uit de beginvoorwaarde voor de snelheid ( 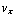 =
= 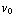 ,
, 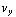 =
= 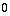 voor t = 0 ) volgt dat α =
voor t = 0 ) volgt dat α = 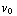 , γ = 0. Als we
, γ = 0. Als we 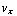 en
en 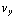 nu invullen in de x- en y-componenten van de krachtenvergelijking b), dan vinden we nog dat δ = -
nu invullen in de x- en y-componenten van de krachtenvergelijking b), dan vinden we nog dat δ = -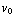 , β = 0.
, β = 0.
2.1.4
a) Er is geen kracht, Het lijkt of degene die dit zegt beweert dat er een kracht qB is. Er zou wel een qE zijn, maar bij magneetvelden is de kracht evenredig met q (![Overscript[B, ->]](HTMLFiles/e+m_366.gif) x
x ![Overscript[v, ->]](HTMLFiles/e+m_367.gif) ). Er is geen stroom (oftewel een snelheid
). Er is geen stroom (oftewel een snelheid ![Overscript[v, ->]](HTMLFiles/e+m_368.gif) ) in het ringetje, en zeker geen stroom loodrecht op het magneetveld van de draad.
) in het ringetje, en zeker geen stroom loodrecht op het magneetveld van de draad.
b) Ten eerste is het een wisselstroom, zodat er niet een constant veld is, ten tweede lopen in een snoer van een wasmachine twee draden, naar de machine en er vanaf, met tegengestelde stroomrichtingen. De bijbehorende magneetvelden heffeb elkaar weliswaar niet helemaal op, maar ze werken elkaar wel tegen.
2.1.5
a) Puntlading: als 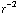 , dipool als
, dipool als 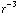 .
.
Een kringstroompje is een magnetische dipool. Als je in de uitdrukking voor het veld op de as z veel groter maakt dan de straal van de lus, zie je dat het veld afvalt als 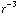 . Twee elkaar tegenwerkende lusjes op enige afstand van elkaar zal leiden tot een afvallen met
. Twee elkaar tegenwerkende lusjes op enige afstand van elkaar zal leiden tot een afvallen met 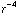 (zie ook opdracht 12 van dagdeel 2 van de elektrostatica opgaven).
(zie ook opdracht 12 van dagdeel 2 van de elektrostatica opgaven).
2.3.1
a) ![Overscript[∂, ->] × ( 2 z , 3 y , -x)](HTMLFiles/e+m_373.gif) = ( 0-0 , 2 - -1 , 0-0 ) = ( 0 , 3 , 0 )
= ( 0-0 , 2 - -1 , 0-0 ) = ( 0 , 3 , 0 )
b) ![Overscript[∂, ->]](HTMLFiles/e+m_374.gif) × (
× ( 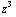 , 0 , 10 ) = ( 0-0 , 3
, 0 , 10 ) = ( 0-0 , 3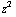 - 0 , 0-0 )
- 0 , 0-0 )
2.3.2
Het veld van een puntlading is: E = 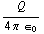 ( x / (
( x / (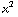 +
+ 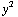 +
+ 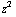
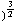 , y / (
, y / (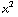 +
+ 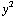 +
+ 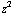
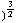 , z / (
, z / (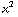 +
+ 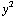 +
+ 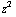
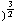 ). Rotatie nemen levert:
). Rotatie nemen levert:
![Overscript[∂, ->]](HTMLFiles/e+m_390.gif) ×
× ![Overscript[E, ->]](HTMLFiles/e+m_391.gif) =
= 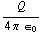 ( (3yz - 3yz) / (
( (3yz - 3yz) / (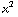 +
+ 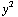 +
+ 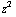
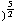 , (3xz - 3xz) / (
, (3xz - 3xz) / (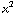 +
+ 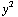 +
+ 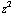
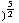 , (3xy - 3xy) / (
, (3xy - 3xy) / (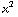 +
+ 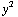 +
+ 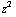
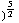 ) = ( 0 , 0 , 0 ).
) = ( 0 , 0 , 0 ).
2.3.3
![Overscript[B, ->]](HTMLFiles/e+m_405.gif) =
= 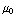
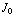 (
( 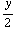 -
- 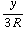
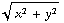 , -
, - 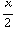 +
+ 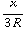
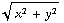 , 0 )
, 0 )
![Overscript[J, ->]](HTMLFiles/e+m_414.gif) =
= 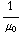
![Overscript[∂ , ->]](HTMLFiles/e+m_416.gif) ×
× ![Overscript[B, ->]](HTMLFiles/e+m_417.gif) =
= 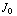 ( 0 , 0 , -
( 0 , 0 , - 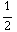 +
+ 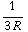
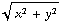 +
+ 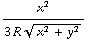 - (
- ( 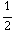 -
- 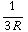
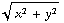 -
- 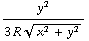 ) ) =
) ) = 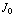 ( 0 , 0 , -1 +
( 0 , 0 , -1 + 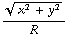 ).
).
Dus J(r) = 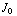 (1 - r/R ). Dit lijkt op de ladingsdichtheid van opgave 8 in dagdeel 2 van de elektrostatica opgaven.
(1 - r/R ). Dit lijkt op de ladingsdichtheid van opgave 8 in dagdeel 2 van de elektrostatica opgaven.
2.3.4
a) Het beschreven B-veld wordt gegeven door: ![Overscript[B, ->]](HTMLFiles/e+m_430.gif) =
= 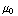 ( y
( y 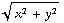 , -x
, -x 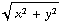 , 0 ).
, 0 ).
![Overscript[J, ->]](HTMLFiles/e+m_434.gif) = ( 0 , 0 , -
= ( 0 , 0 , - 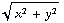 -
- 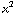 /
/ 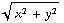 - (
- ( 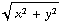 +
+ 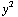 /
/ 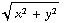 ) ) = ( 0 , 0 , - 2r - r ) = ( 0 , 0 , - 3r ).
) ) = ( 0 , 0 , - 2r - r ) = ( 0 , 0 , - 3r ).
b) Neem een cirkel rond de z-as met straal r. De totale stroom die daar doorheen loopt is: I = 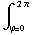
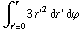 = 2π
= 2π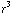 . Verder is
. Verder is ![∫ Overscript[B, ->] * Overscript[dl, ->]](HTMLFiles/e+m_444.gif) = 2πr B.
= 2πr B.
Dus B = 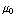
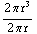 =
= 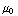
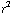 . Klopt!
. Klopt!
2.3.5
a) Links van alle platen is het B-veld 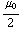 (
(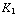 +
+ 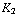 +
+ 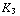 ) Tesla, tussen de linker- en de middelste plaat
) Tesla, tussen de linker- en de middelste plaat 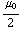 (-
(- 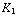 +
+ 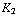 +
+ 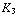 ) Tesla, en tussen de middelste en de rechter plaat
) Tesla, en tussen de middelste en de rechter plaat 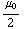 (-
(- 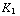 -
- 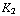 +
+ 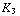 )Tesla. Hieruit kun je
)Tesla. Hieruit kun je 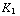 ,
, 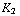 en
en 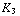 oplossen:
oplossen: 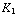 = 2,4
= 2,4 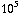 A,
A, 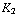 = 4,8
= 4,8 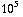 A, en
A, en 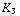 = 8,8
= 8,8 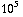 A.
A.
b) Het veld rechts van de rechter plaat is precies tegengesteld aan het veld links van de linker plaat.
2.3.6
a) Om het B-veld te berekenen nemen we een rechthoek. Een zijde (lengte a, met a<<l) ligt langs de as van de spoel. De andere zijde met lengte a ligt buiten de spoel, en de twee resterende zijden met lengte b staan (uiteraard) loodrecht op de as van de spoel. Laat nu b naar oneindig gaan, dan ligt een van de zijden met lengte a oneindig ver weg en is het B-veld daar nul, zodat dat stuk niet zal bijdragen in de kringintegraal van B. De twee stukken loodrecht op de cylinder-as leveren ook niks op, want uit de symmetrie volgt dat de radiele component van ![Overscript[B, ->]](HTMLFiles/e+m_470.gif) nul is. Verder is het B-veld in de spoel homogeen dus we krijgen:
nul is. Verder is het B-veld in de spoel homogeen dus we krijgen: ![∫ Overscript[B, ->] Overscript[dl, ->]](HTMLFiles/e+m_471.gif) = aB. De ingesloten stroom in het loopje is aNI. Het B-veld wordt dus: B =
= aB. De ingesloten stroom in het loopje is aNI. Het B-veld wordt dus: B = 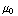 NI.
NI.
b) Neem nu als loop een cirkel langs de hartlijn van de donut. De lengte van de loop is dus 2πR, met R de straal van de donut. We krijgen nu: ![∫ Overscript[B, ->] Overscript[dl, ->]](HTMLFiles/e+m_473.gif) = 2πR B =
= 2πR B = 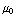 2πR NI, dus B =
2πR NI, dus B = 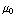 NI. Dit is hetzelfde als bij de spoel. Een donut is in feite een lange spoel waarvan het begin en het einde aan elkaar zijn 'geplakt'.
NI. Dit is hetzelfde als bij de spoel. Een donut is in feite een lange spoel waarvan het begin en het einde aan elkaar zijn 'geplakt'.
Converted by Mathematica
(June 20, 2003)
![[Graphics:HTMLFiles/e+m_49.gif]](HTMLFiles/e+m_49.gif)
![[Graphics:HTMLFiles/e+m_119.gif]](HTMLFiles/e+m_119.gif)